中2数学「2学期期末テスト予想問題(解答・解説付)」です。今回は、図形の証明、角度を中心にもう台を構成しています。
【中2数学・問題】2学期期末テスト予想問題
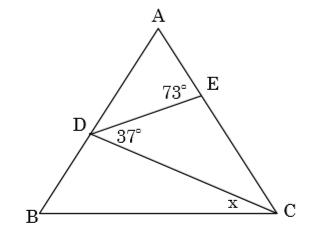
【問1 角度】図で、△ABCは正三角形、D、Eはそれぞれ辺AB、辺AC上の点である。∠AED=73°、∠EDC=37°のとき、∠DCBの大きさを求めよ。
【問2 証明】次の問いに答えなさい。
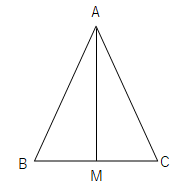
(1)「二等辺三角形の底角は等しい。」という性質を証明したい。図のようにAB=ACの二等辺三角形がある。辺BCの中点をMとするとき∠ABM=∠ACMとなることを証明せよ。
(2)△ABCで、∠B=∠Cとすると、△ABCはAB=ACの二等辺三角形となることを証明せよ。

(3)図のAB=ACの二等辺三角形でAMが頂角∠BACの二等分線である。このとき、△ABM≡△ACMを証明せよ。

【問3 いろいろな四角形】次の図の平行四辺形ABCDに、次の条件が加わると、それぞれどんな四角形になるか、答えよ。
(1)AC=BD
(2)AO⊥BD
(3)AO=DO,AC⊥DO
【中2数学・解答解説】2学期期末テスト予想問題
【問1】24°
三角形の内角と外角の関係
角の1つの辺を延長し、そのとなりの辺との間にできる角を、その頂点における外角といいます。外角に対して、△ABCの3つの角、∠A、∠B、∠Cを内角といいます。
- 三角形の内角の性質…三角形の内角の和は180°です。
- 三角形の外角の性質…三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。
鋭角と鈍角
- 鋭角…0°より大きく90°より小さい角を鋭角といいます。
- 鈍角…90°より大きく180°より小さい角を鈍角といいます。
三角形の分類
- 鋭角三角形…3つの内角がすべて鋭角である三角形
- 直角三角形…1つの内角が直角である三角形
- 鈍角三角形…1つの内角で鈍角である三角形
【問2】
(1)△ABMと△ACMにおいて
AB=AC(仮定)
BM=CM(MはBCの中点)
AMは共通
よって三辺がそれぞれ等しいので
△ABD≡△ACD
対応する角は等しいので∠ABD=∠ACD
(2)∠Aの二等分線をひき、BCとの交点をDとします。
△AMBと△AMCで
仮定より、∠ABM=∠ACM …①
仮定より ∠BAM=∠CAM …②
三角形の3つの内角の和が180°であることと①②より
∠AMC=∠AMC…③
共通な辺より AM=AM…④
②③④より 1組の辺とその両端の角がそれぞれ等しいので、
△AMB≡△AMC
合同な図形では、対応する辺は等しいので。
AB=AC
(3)△ABMと△ACMにおいて
AB=AC(仮定)
∠BAD=∠CAD(AMは∠BACの二等分線)
AM=AM(共通)
よって二辺とその間の角がそれぞれ等しいので
△ABM≡△ACM
二等辺三角形について
- 二等辺三角形の定義…2つの辺が等しい三角形(※定義は、使う言葉の意味をはっきり述べてものです。)
- 二等辺三角形の性質…二等辺三角形の2つの定角は等しい。
- 二等辺三角形の定理①二等辺三角形の2つの定角は等しい。
- 二等辺三角形の定理②…二等分線は、底辺を垂直に2等分する。
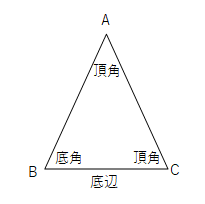
AB=ACである二等辺三角形ABCで等しい辺のつくる∠Aを頂角、頂角に対する辺BCを底辺、底辺の両端の角∠B、∠Cを定角といいます。
【問3】
(1)長方形
(2)ひし形
(3)長方形
長方形・ひし形・正方形
- 長方形…4つの角がすべて等しい四角形
- ひし形…4つの辺がすべて等しい四角形
- 正方形…4つの辺、4つの角がすべて等しい四角形
正方形は、長方形とひし形を足したものですね。
平行四辺形との関係
長方形、ひし形、長方形は、すべて平行四辺形である。よって、長方形・ひし形・正方形は、これらの四角形は、平行四辺形の性質をもっています。
四角形の対角線の性質
- 長方形の対角線は、長さが等しい。
- ひし形の対角線は、垂直に交わる。
- 正方形の対角線は、長さが等しい、垂直に交わる。
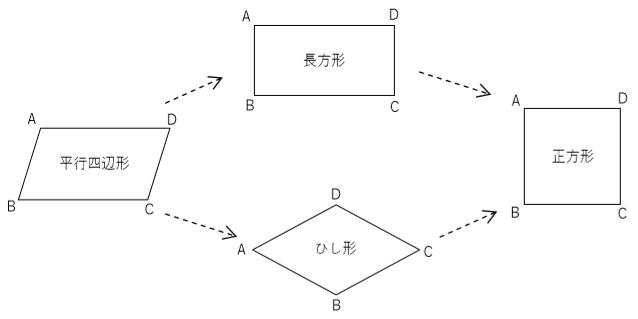
- 長方形は、平行四辺形から、∠Aが90°、または、∠A=∠B、AC=BDなどになれば、長方形になる。
- ひし形は、AB=BC、AC⊥BDなどの条件があてはまる。
- 正方形は、長方形とひし形の性質をあわせもつ。


コメント