中2数学学年末テスト予想問題と解答解説です。
学年末テスト予想問題(中2数学)
➊次の( )にあてはまる最も適当なことばを答えなさい。ただし、ことばは、漢字ですべて書きなさい。
(1)使うことばの意味をはっきりのべたものを( ア )という。また、証明されたことがらのうち、基本になるものを定理という。
(2)二等辺三角形の( イ )の二等分線は、( ウ )を垂直に2等分する。
(3)直角三角形で、直角に対する辺を( エ )という。
(4)二等辺三角形になるための条件は、「( オ )は、二等辺三角形である。」
(5)正三角形の定義は、「( カ )を正三角形という」
(6)平行四辺形の性質を3つそれぞれ書きなさい。( キ )( ク )( ケ )
➋次のことがらの逆を言いなさい。また、それが正しいかどうか調べ、正しくない場合には反例を示しなさい。
(1)a>0、b>0ならば、a+b>0である。
(2)△ABCで、AB=ACならば、∠B=∠Cである。
(3)∠B=90°の△ABCで、AB=6cm、BC=4cmならば、面積は12cm2である。
(4)△ABCと△DEFで、△ABC≡△DEFならば、AB=DE、BC=EF、∠B=∠Eである。
(5)整数a,bで、aもbも偶数ならば、abは4の倍数です。
➌次の図の三角形の中から、合同な三角形の組を3つ選びなさい。またそのときの合同条件も書きなさい。
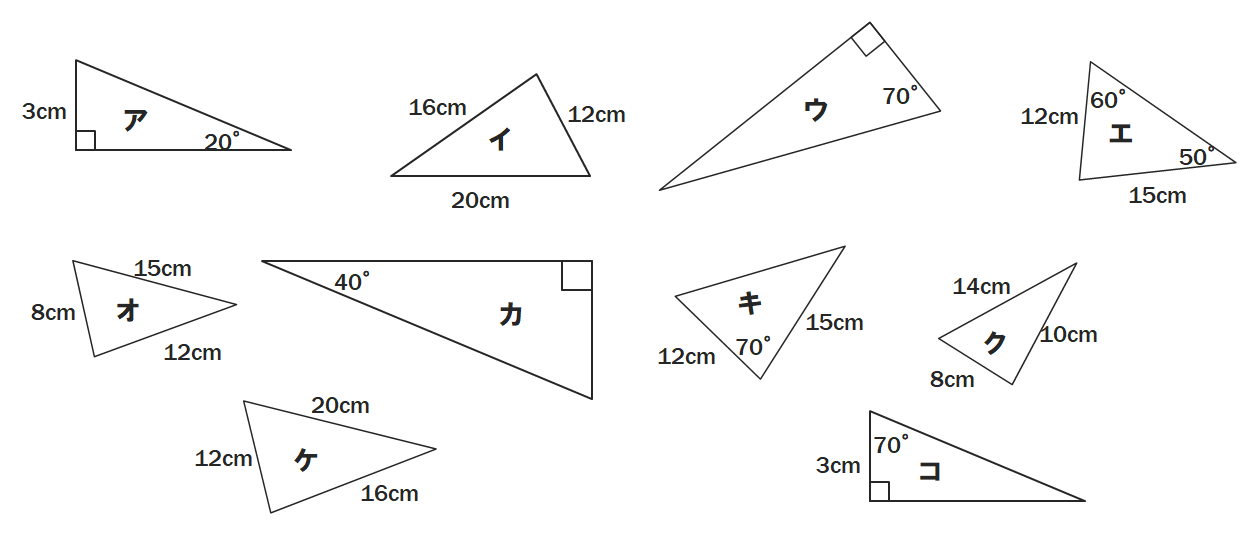
➍AB=ACであり、頂角∠BACが鈍角である二等辺三角形ABCがある。下の図のように、辺BAの延長線上にCA=CDとなる点Dをとる。∠ACD=16°のとき、∠ABCを求めなさい。
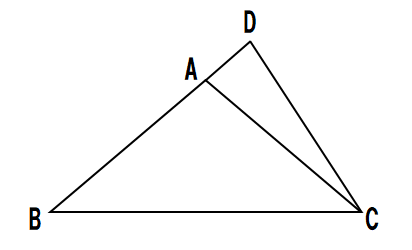
➎次の図の∠x の大きさを求めなさい。( OA=AB=BC=CD )
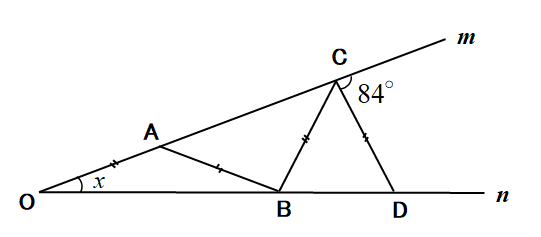
➏∠xの大きさを求めよ。ただし、同じ印をつけた角は等しい。
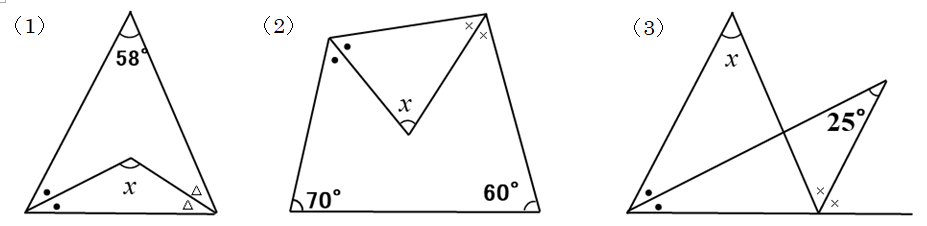
➐次の図の平行四辺形ABCDで、∠xの大きさを求めなさい。
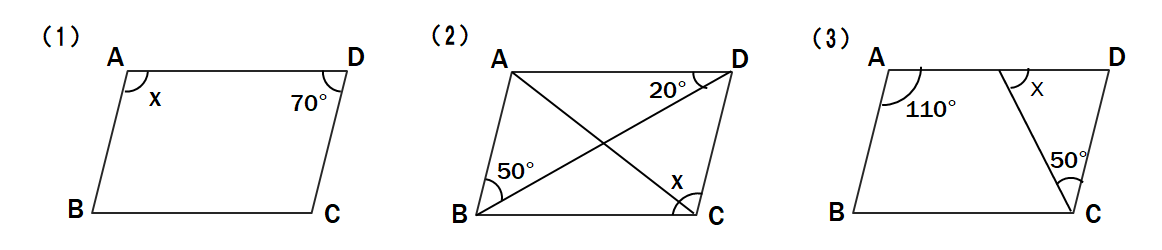
➑次の図で線分ABの中点をMとし、Mを通る線分CDを∠CAM=∠DBMとなるようにとると、AC=BDであることを証明せよ。
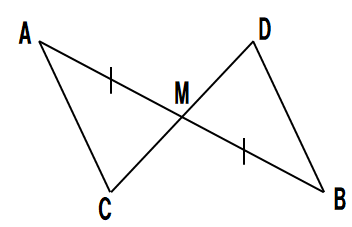
➒次の図で、AB=ACの二等辺三角形ABCで、頂点Bから辺ACに垂線をひき、その交点をD、また、頂点Cから辺ABに垂線をひき、その交点をEとします。このときAD=AEになることを証明せよ。
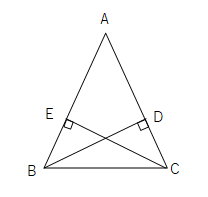
➓AB=ACの二等辺三角形ABCで、辺AB,ACの中点を、それぞれM、Nとします。BNとCMの交点をPとするとき、△PBCは二等辺三角形であることを証明せよ。

⓫次の図の平行四辺形ABCDの対角線BD上に、点E、FをBE=DFとなるようにとります。このとき、AE=CFであることを証明せよ。
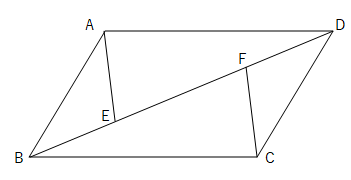
⓬平行四辺形ABCDで、辺ABをBの方に延長した直線上に点Eをとり、線分DEと辺BCとの交点をFとします。線分AF,BD,ECをひくとき、△BECと面積の等しい三角形をすべて見つけなさい。
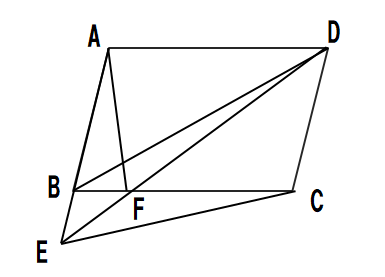
⓭次の条件のとき、四角形ABCDは平行四辺形になるかどうか答えよ。
(1)∠A=∠C、∠B=∠D
(2)AB=BC、CD=DA、∠A=100°、∠B=70°
(3)BC//DA、AB=CD=6cm
学年末テスト予想問題の解説・解答(中2数学)
➊
ア:定義
イ:頂角
ウ:底辺
エ:斜辺
オ:2つの角が等しい三角形
カ:3つの辺が等しい三角形
キ:2組の対辺はそれぞれ等しい
ク:2組の対角はそれぞれ等しい
ケ:対角線はそれぞれの中点で交わる
(キとクとケは順不同)
➋
(1)a+b>0ならば、a>0、b>0である。 正しくない。(反例)a=2,b=-1
(2)△ABCで、∠B=∠Cならば、AB=ACである。 正しい。
(3)∠B=90°で、△ABCで、面積が12cm2ならば、AB=6cm、BC=4cmである。 正しくない。(反例)AB=2cm、BC=12cm
➌
アとコ 直角三角形の斜辺と1つの鋭角がそれぞれ等しい
イとケ 3組の辺がそれぞれ等しい
エとキ 2組の辺とその間の角がそれぞれ等しい
➍41°
➎21°
➏(1)119° (2)65° (3)50°
➐(1)110° (2)110° (3)60°
➑
△CAMと△DBMにおいて
仮定より AM=BM…①
仮定より ∠CAM=∠DBM…②
対頂角より∠AMC=∠BMD…③
①②③より、1辺とその両端の角がそれぞれ等しいので
△CAM≡△DBM
合同な図形の対応する辺は等しいので
AC=BD
➒
△ABDと△ACEにおいて
仮定より AB=AC…①
仮定より ∠ADB=∠AEC=90°…②
共通な角より ∠BAD=∠CAE…③
①②③より 直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△ABD≡△ACE
合同な図形は対応する辺は等しいので、AD=AE
➓
△MBCと△NCBにおいて
仮定より、MB=MC…①
二等辺三角形ABCの性質より、∠MBC=∠NCB…②
共通の辺より、BC=CB…③
①②③より、2辺とその間の角がそれぞれ等しいので
△MBC≡△NCB
合同な図形は対応する角は等しいので、∠MCB=∠NBC
よって、2つの角がそれぞれ等しくなるので、△PBCは二等辺三角形となる。
⓫
△ABEと△CDFで、
仮定より、BE=DF…①
AB//DCより錯角が等しいので、∠ABE=∠CDF…②
平行四辺形の向かい合う辺は等しいので、AB=CD…③
①②③より2組の辺とその間の角がそれぞれ等しいので
△ABE≡△CDF
合同な図形では、対応する辺は等しいので、AE=CF
⓬△BED、△AEF
⓭(1)平行四辺形になる(2)平行四辺形にならない (3)平行四辺形にならない

コメント