中2数学「確率の練習問題」ポイント解説付です。
【問題】確率の練習問題
【問1】次の問いに答えなさい。
- A,B,C,Dの4人がリレーで走ります。1番最初にBかCが走るとすると、走る順番は何通りありますか?
- 1,2,3,4と書かれた4枚のカードがあります。このカードのうち。3枚を並べてできる3けたの整数は、全部で何個ですか。
- バレーボールの試合で、A,B,C,Dの4チームがそれぞれ1回ずつ対戦するときの試合数を求めなさい。
- 1つのさいこを投げるとき、2つの目が出る確率を求めなさい。
- 赤玉1個、白玉3個、青玉4個がはいっている袋から白玉を1個取り出すときの確率を求めなさい。
- 赤玉だけが8個はいっている袋から玉を1個取り出すとき赤玉が出る確率を求めなさい。
- ジョーカーを除く1組52枚のトランプをよくきって、そこから1枚をひくとき、ハートの札が出る確率を求めなさい。
- 1から20までの数字が1つずつ書かれた20枚のカードがあります。このカードをよくきって、そこから1枚をひくとき、カードに書かれている12以上の確率を求めなさい。
【問2】次の問いに答えよ。
- 2枚のコインを同時に投げるとき、2枚とも表になる確率を求めよ。
- 2枚のコインを同時に投げるとき、2枚とも裏になる確率を求めよ。
- 2枚のコインを同時に投げるとき、1枚が裏になる確率を求めよ。
- 2枚のコインを同時に投げるとき、少なくとも1枚が裏になる確率を求めよ。
- 3枚の硬貨を同時に投げるとき、3枚とも表になる確率を求めよ。
- 3枚の硬貨を同時に投げるとき、3枚とも裏になる確率を求めなさい。
- 3枚の硬貨を同時に投げるとき、1枚が表になる確率を求めなさい。
- 3枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
- 4枚の硬貨を同時に投げるとき、4枚とも表になる確率を求めよ。
- 4枚の硬貨を同時に投げるとき、少なくとも1枚が表になる確率を求めなさい。
【問3】
1個のサイコロを投げるとき、次の確率を求めなさい。
①2の目が出る確率
②3または4の目が出る確率
③3以下の目が出る確率
④3より小さい目が出る確率
⑤2以外の目が出る確率
⑥偶数の目が出る確率
【問4】
大小2つのサイコロを同時に投げる。大きいほうのサイコロの目をa、小さいほうのサイコロの目をbとする。このとき、次の問いに答えなさい。
(1)a-b=1となる確率を求めなさい。
(2)aとbの差が2となる確率を求めなさい
(3)2a=bとなる確率を求めなさい。
【問5】
当たりが2本、はずれが3本入っているくじがある。このくじを同時に2本ひくとき答えなさい。
①2本とも当たりである確率を求めなさい。
②2本ともはずれである確率を求めなさい。
③少なくとも1本は当たりである確率を求めなさい。
【問6】
8本中に当たりが3本入っているくじがある。このくじをまずAが引いて次にBが引くとき、次の問いに答えさい。
①Aが当たる確率を求めなさい。
②AがはずれてBが当たる確率を求めなさい。
③AもBも当たる確率を求めなさい。
【問7】
下の図のように、袋A,袋Bがある。袋Aには、1,2,3,4,5の数が書かれた玉が1個ずつ入っており、袋Bには、1,2,3,4,5,6の数が書かれた玉が1個ずつ入っている。袋Aから玉を1個、袋Bから玉を1個、合計2個の玉を取り出し、袋Aから取り出した玉に書かれている数をa、袋Bから取り出した玉に書かれている数をbとする。このとき、a>bとなる確率と(a-2)(b-3)=2となる確率のどちらが起こりやすいか、それぞれの確率を示し求めよ。

【問8】図のように、1~4までの番号のついた4つの箱と、1~4までの数字が1つずつ書かれた4個の玉が入った袋がある。袋の中から玉を1個ずつ4個続けて取り出し、取り出した順に1番の箱,2番の箱,3番の箱,4番の箱に入れる。このとき、次のア~ウのことがらのうち、最も起こりやすいことがらが起こる確率を求めよ。ただし、どの玉を取り出すことも同様に確からしいものとする。
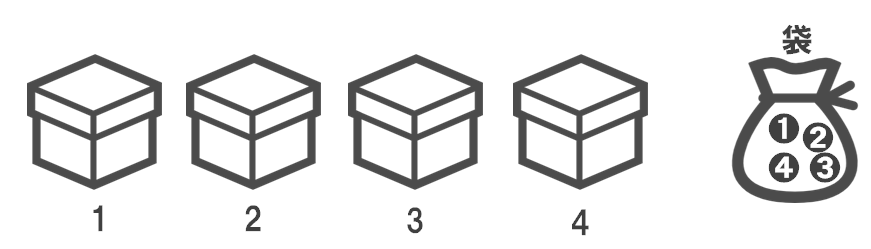
ア:箱の番号とその箱に入った玉の数字がどの箱も異なる。
イ:箱の番号とその箱に入った玉の数字が一致する箱が1つだけある。
ウ:箱の番号とその箱に入った玉の数字が一致する箱が2つある。
【解答】確率の練習問題
【問1】
- 12通り
- 24個
- 6試合
- 1/6
- 3/8
- 1
- 1/4
- 9/20
【問2】
- 1/4
- 1/4
- 1/2
- 3/4
- 1/8
- 1/8
- 3/8
- 7/8
- 1/16
- 15/16
【問3】
①1/6
②1/3
③1/2
④1/3
⑤5/9
⑥1/2
【問4】
(1)5/36
(2)2/9
(3)1/12
【問5】
①1/10
②3/10
③7/10
【問6】
①3/8
②15/56
③3/28
【問7】
すべての場合の数は、30通り
a>bとなる確率は、
条件を満たす(a,b)が(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(5,1)(5,2)(5,3)(5,4)の10通りで
求める確率は10/30=1/3
(a-2)(b-3)=2となる確率は、
条件を満たす(a,b)が(1,1)(3,5)(4,4)の3通りで
求める確率は3/30=1/10
よって、起こりやすいのはa>bとなる確率
【問8】
アが起こる確率は3/8
イが起こる確率は1/3
ウが起こる確率は1/4
よって、アの起こる確率が最も起こりやすい。
確率のポイント
あることがの起こりやすさの程度を表す数を、そのことがらの起こる確率といいます。実際に実験を行う場合、回数が少ないうちは、相対度数のばらつきは大きいが、回数が多くなると、そのばらつきは小さくなり、一定の値に近づく。
場合の数とは?
起こりうる場合が、すべてでn通り(=場合の数)あり、そのどれが起こることも同様に確からしいとする。ことがらAの起こる場合がn通りあるとき、Aの起こる確率pはp=a/nとなります。
- 場合の数…起こりうる場合が、すべてでn通りのときのように、起こりうるすべての数を場合の数といいます。
- 確率…あることがらの起こることが期待される程度を表す数を、そのことがらを起こる確率といいます。
- 同様に確からしい…さいころの目の出かたは、1から6までの6通りあり、どの目が出ることも同じ程度に期待されます。このような、どの目が出ることも同様に確からしいといいます。
硬貨・コインの確率
硬貨・コインは、以下のように樹形図を書いて求めてます。
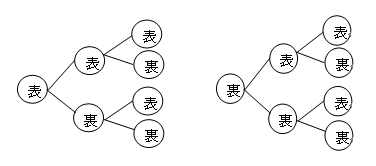
余事象(少なくとも)
3枚の効果を投げて、「少なくとも2枚は表」とは、3枚とも表、または、2枚は表で、1枚は裏の場合のこと。「少なくとも1枚は表」とは、3枚とも表、2枚は表で1枚は裏、1枚は表で2枚は裏の場合のこと。すなわち、すべて以外の場合といえる。
さいころの確率
さいころは、一般的に
- 1つのさいころをなげるとき、場合の数は6通り
- 2つのさいころをなげるとき、場合の数は36通りで、表で解く
- 3つのさいことをなげるとき、場合の数は216通り=6の3乗
の3つのパターンがよく出題されます。
表の書き方
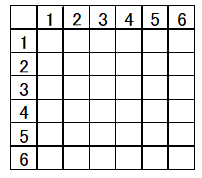
玉・くじの確率
樹形図を書くことが、大前提です。それに基づいて、解いていきます。そこで大事なのは、組み合わせなのか、順列(順番が関係するのか)を問題から読み取り、樹形図を書いていきましょう。組み合わせは、A-BとB-Aは、同じなので、B-Aの樹形図は書く必要がありません。

コメント