中学1年理科。大地の変化「地震」の計算特訓を行います。
- 重要度★★★☆
- レベル★★★☆
- ポイント:4つの計算パターンをマスターする!
授業用まとめプリントは下記リンクからダウンロード!
授業用まとめプリント「地震の計算」
地震の計算
地震の単元では、計算問題がよく出題されます。簡単な速さの計算から、初期微動継続時間の性質を使った計算、さらには、大森公式を使って計算する問題など様々な計算方法があります。
しかし、これらの計算問題を分析すると、大きく4つのグループに分けることができます。今日はこの4つの計算方法をマスターしましょう。
地震の計算の4つのパターンは次の通りです。
- P波とS波の速さの計算
- 地震発生時刻の計算
- 初期微動継続時間の計算
- 大森公式を使った計算
4は発展内容になるので今回は省略します。それでは、3つの計算方法を見ていきましょう。
P波とS波の速さの求め方
一番オーソドックスな地震の計算です。速さを求めるのですから、距離と時間を読み取り、
距離÷時間=速さ
で求めることができます。グラフや表で数値が与えられるので、必要な数字を読み取り計算できるように練習しましょう。
●グラフから地震の速さを求める
地震のグラフからP波やS波の速さを求めてみましょう。下のグラフは、初期微動を伝える波(P波)と、主要動を伝える波(S波)の伝わり方を表しています。
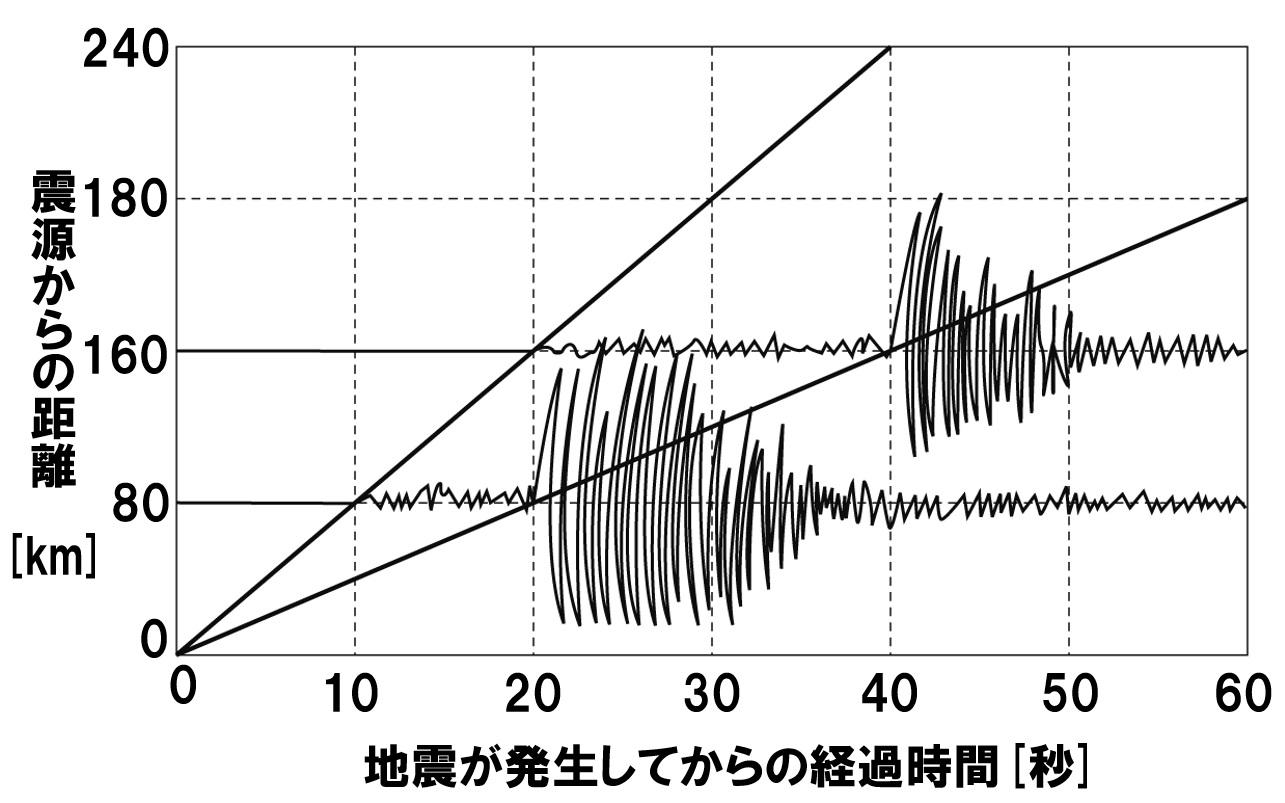
傾きが大きく、速く伝わっているほうがP波、傾きが小さく、遅く伝わっているほうがS波になります。グラフの場合、グラフの格子点を通っている2点を探し出し、その2点間の距離と、2点間の地震波の到着時刻の差で速さを計算します。
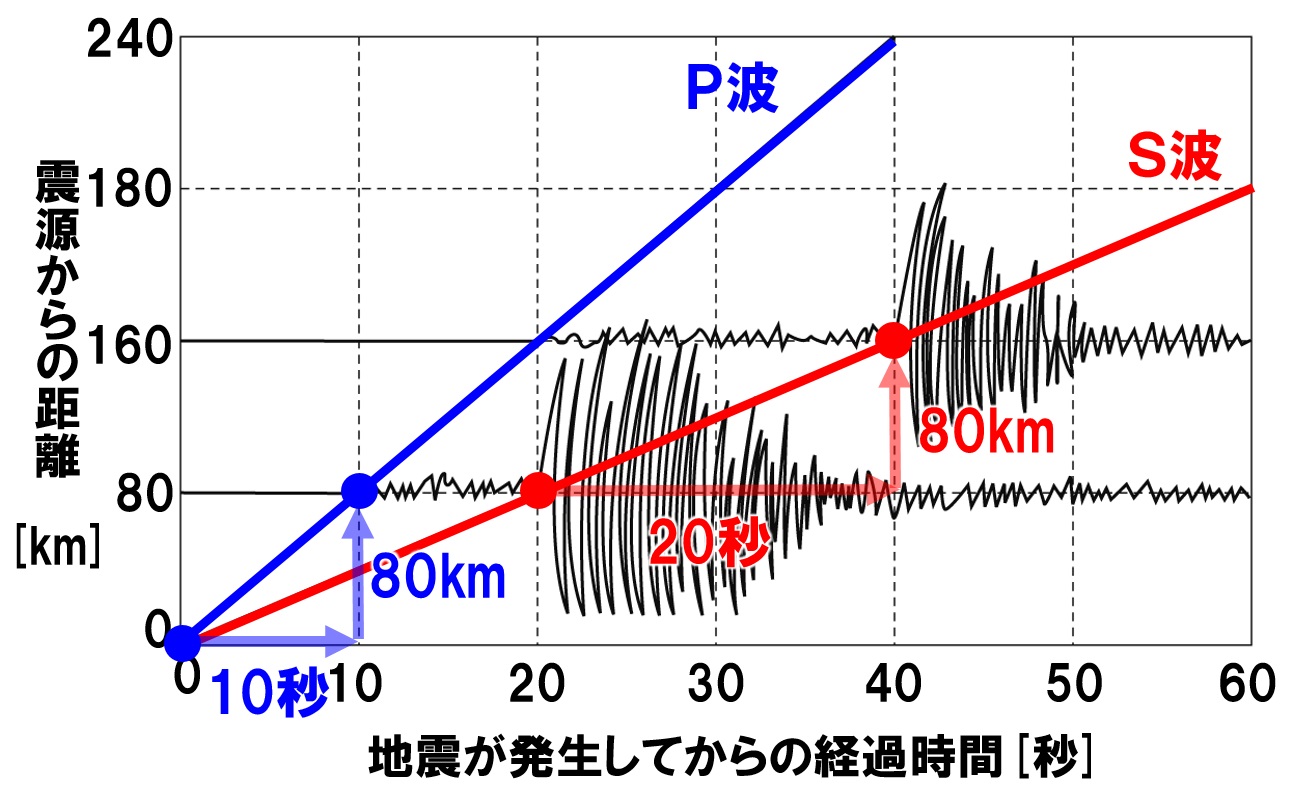
P波:グラフより、80kmの道のりを10秒かかっているとわかりますので、
80km÷10秒=8km/s
S波:グラフより、80kmの道のりを20秒かかっているとわかりますので、
80km÷20秒=4km/s
と計算できます。グラフの2点がわかれば速さが計算できます。
●表から地震の速さを求める
グラフではなく、表で情報を与えられる場合もあります。
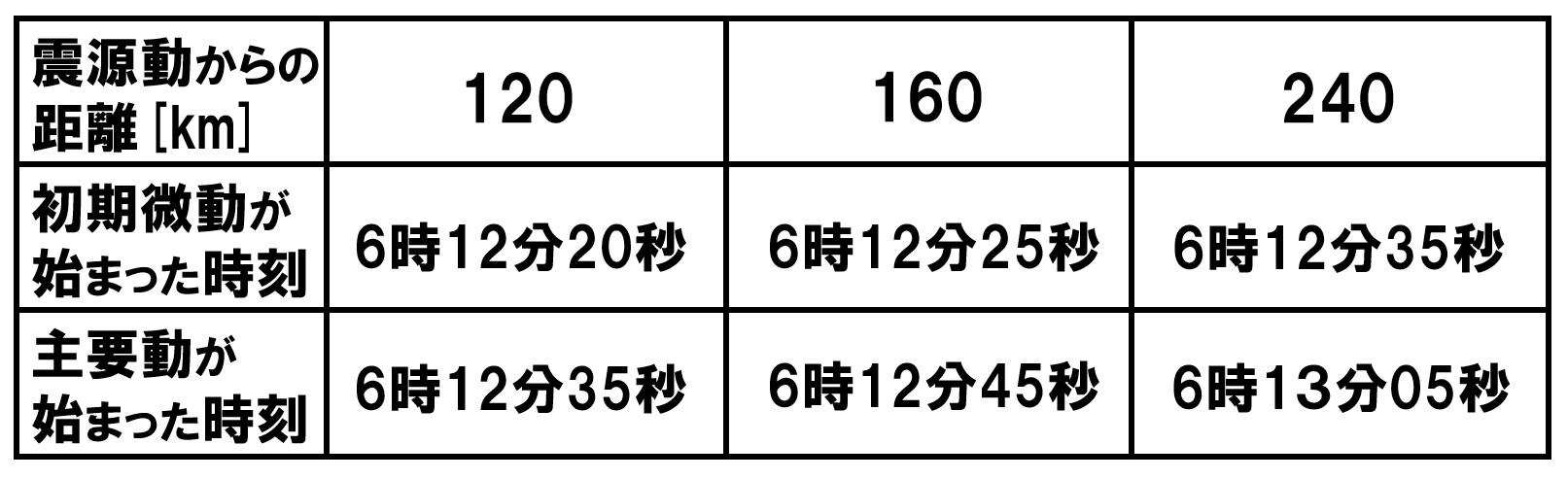
この場合も、2点間の距離と、ゆれが始まった時刻の差から地震波の速さを求めます。
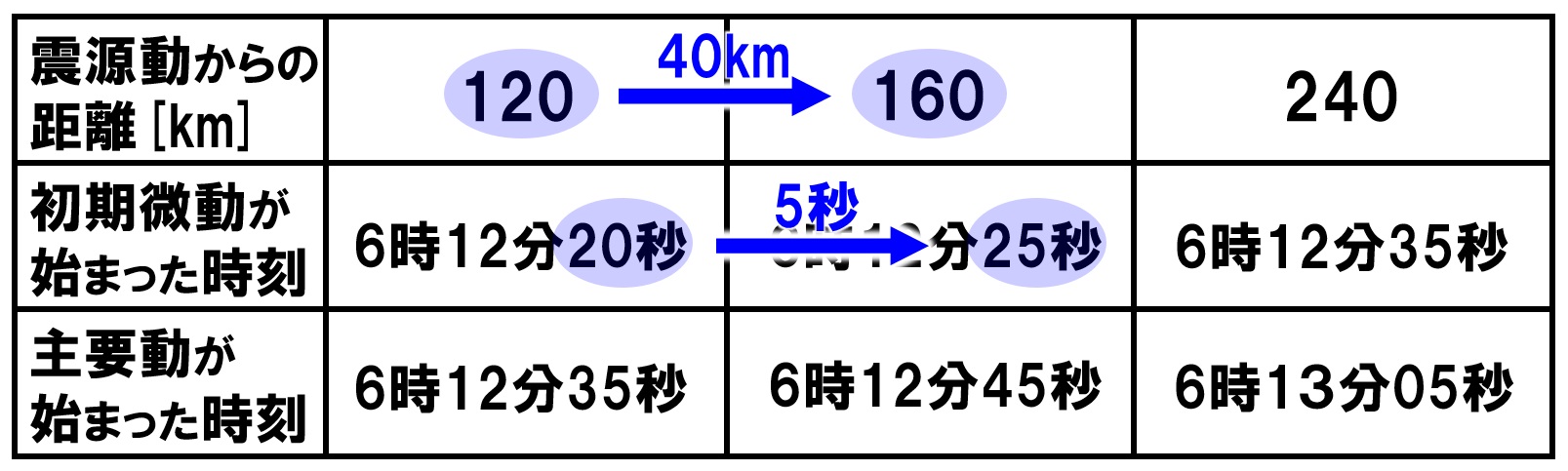
P波:表より、40kmの道のりを5秒かかっていることがわかります。
40km÷5秒=8km/s
次はS波を求めます。
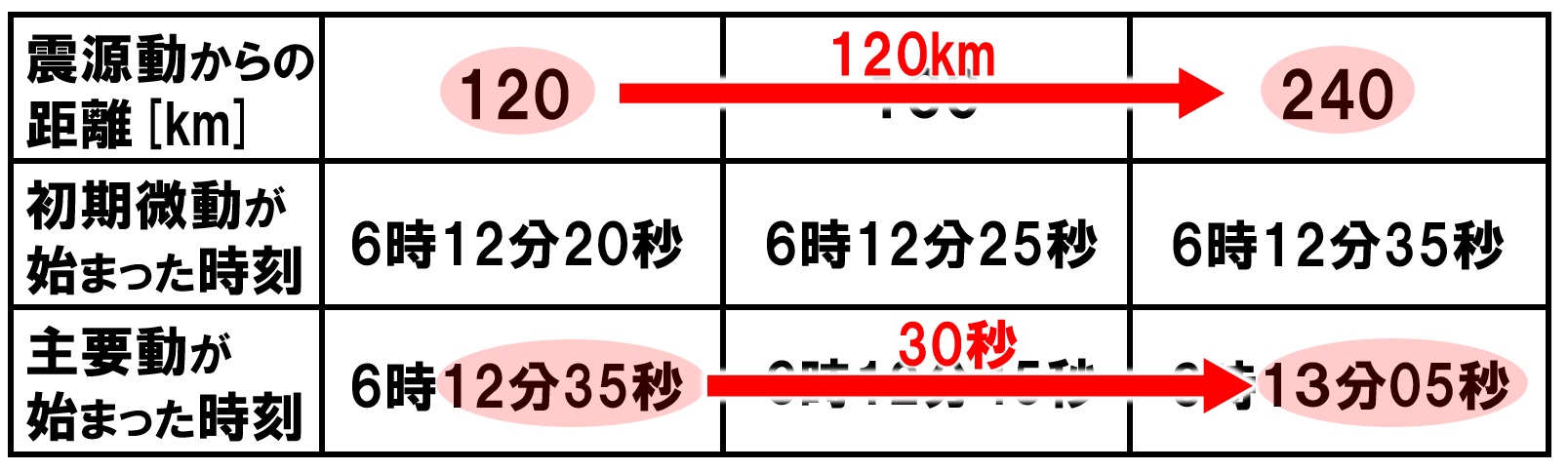
S波:表より、120kmの道のりを30秒かかっているとわかります。
120km÷30秒=4km/s
グラフとやり方は同じですね。ここは確実に計算できるようになっておきましょう。
次の表は、ある地点での地震の記録をまとめたものである。この地震のP波とS波の速さを求めよ。
| 観測地点 | A地点 | B地点 |
| 初期微動が始まった時刻 | 10時13分33秒 | 10時13分38秒 |
| 主要動が始まった時刻 | 10時13分43秒 | 10時13分53秒 |
| 震源からの距離 | 60km | 90km |
解答P波:6km/s S波:3km/s
A地点とB地点の距離の差は、90-60=30km
初期微動を起こすP波が、30kmを進むのにかかった時間は、
10時13分38秒-10時13分33秒=5秒
したがってP波の速さは、30km÷5秒=6km/s
A地点とB地点の距離の差は、90-60=30km
主要動を起こすS波が、30kmを進むのにかかった時間は、
10時13分53秒-10時13分43秒=10秒
したがってP波の速さは、30km÷10秒=3km/s
地震発生時刻の求め方
地震発生時刻を求める場合は、まず、地震波の速さを計算し。その速さを使って観測地点まで地震波が到着するのにかかった時間を求めます。観測地点でゆれが始まった時刻から、かかった時間を引けば地震発生時刻が求まるというパターンです。下の表が与えられたときの、地震発生時刻を求めてみましょう。

わかりやすく数直線上にまとめてみます。
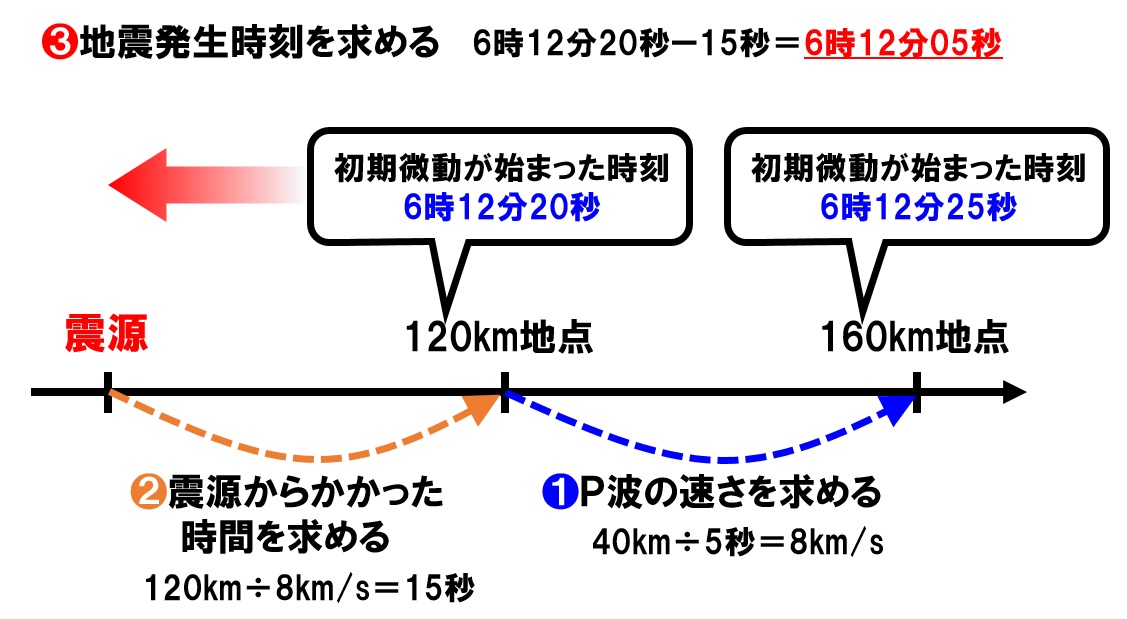
まずは、地震の波の速さを求めます。P波でもS波でも構いません。今回はP波の速さを使って地震発生時刻を求めてみます。
- P波の速さを求める。
120km地点と160km地点から、
40km÷5秒=8km/s - 震源から120km地点までP波がかかった時間を求める。
120km÷8km/s=15秒 - 120km地点にP波が到着した時刻から地震発生時刻を求める。
6時12分20秒-15秒=6時12分05秒
このように、3回ほど計算を繰り返して地震発生時刻を求めていきます。別の方法もありますので、表やグラフから他に計算の方法がないか考えてみるのもいいですね。
次の表は、ある地点での地震の記録をまとめたものである。この地震が発生した時刻を求めよ。
| 観測地点 | A地点 | B地点 |
| 初期微動が始まった時刻 | 10時13分33秒 | 10時13分38秒 |
| 主要動が始まった時刻 | 10時13分43秒 | 10時13分53秒 |
| 震源からの距離 | 60km | 90km |
解答地震発生時刻:10時13分23秒
P波の速さは、
(90km-60km)÷(10時13分38秒ー10時13分33秒)=6km/s
震源からA地点(60km)までP波がかかった時間は、
60km÷6km/s=10秒
A地点にP波が到着した時刻から、かかった時間を引くと、
10時13分33秒ー10秒=10時13分23秒
【別解】A地点とB地点の距離の差は、90-60=30km
初期微動を起こすP波が、30kmを進むのにかかった時間は、
10時13分38秒-10時13分33秒=5秒
震源からA地点まで60km離れているので、P波は震源から10秒かかって到着したと分かる。
10時13分33秒-10秒=10時13分23秒
初期微動継続時間を活用する
P波が到着してからS波が到着するまでの時間を初期微動継続時間といいました。S波が到着し主要動が始まるまで、しばらく初期微動が続きます。この初期微動継続時間は、震源からの距離が遠くなればなるほど長くなっていきました。比例の関係になりましたね。
なので、比例式をつくって計算していきます。下の表で、xとyの値を求めてみましょう。
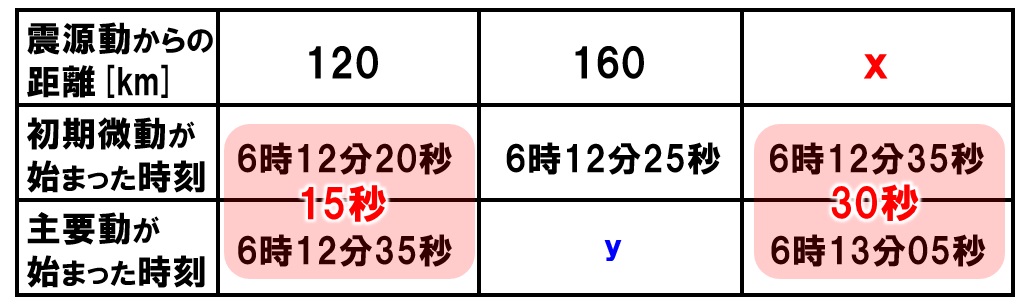
まずはxを求めます。
120km地点での初期微動継続時間は、
6時12分35秒-6時12分20秒=15秒
xkm地点での初期微動継続時間は、
6時13分05秒-6時12分35秒=30秒
初期微動継続時間は、震源からの距離に比例するので、
120km:xkm=15秒:30秒
x=240km
次にyを求めます。
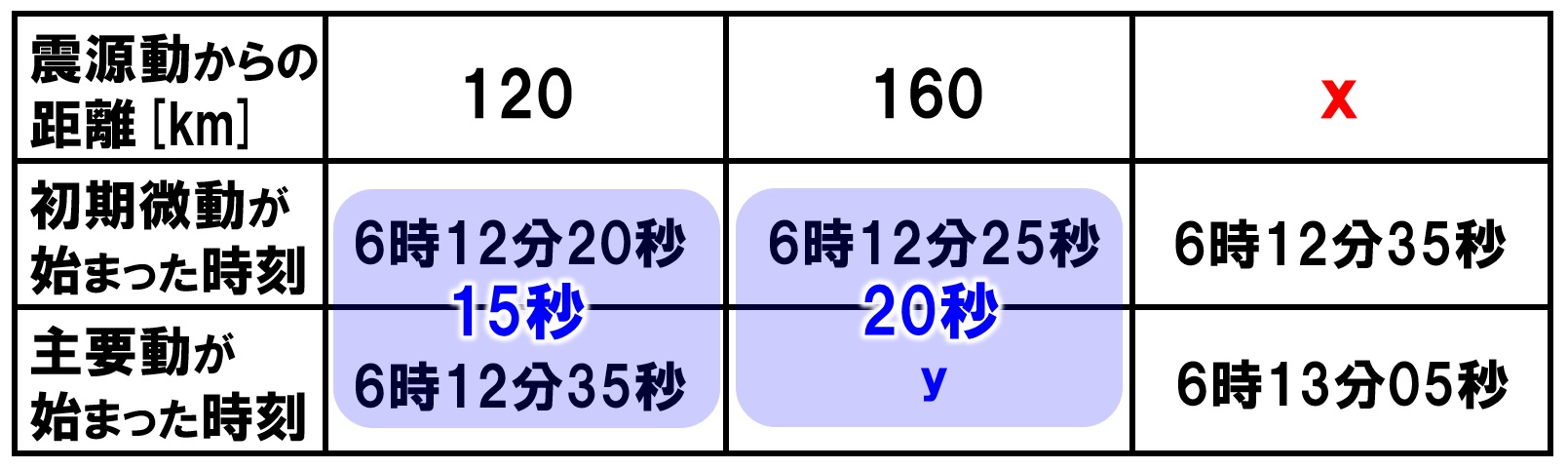
120km地点での初期微動継続時間は、
6時12分35秒-6時12分20秒=15秒
初期微動継続時間は、震源からの距離に比例するので、
120km:160km=15秒:t秒
t=20秒
初期微動継続時間が20秒なので、主要動は初期微動が始まった時刻から20秒遅れて到着します。
6時12分25秒+20秒=6時12分45秒

コメント
めちゃくちゃわかりやすいです。
地震発生時刻のもとめ方わからんかったので助かりました!(テスト前日)