中2数学「一次関数の利用」の練習問題と解説です。「出会いの問題」「点の移動の問題」「料金の問題」と一次関数の利用の代表的な出題パターンから問題は構成されています。
➊単位に気をつける。※速さの単位にそろえる。
➋x軸、y軸が何を表しているかチェック(単位は、速さ・距離・時間ともに、そのx、yにそろえる)
■ 点の移動のポイント
➊グラフや表が用意されていない場合は、題意に沿って自分で用意(作成)して問題を解き始める。
➋面積が同じなどどあれば、交点がその答えとなる。
➌通常、わかっているx,yに相当する値を式に代入すれば、解答を導ける。
一次関数の利用の練習問題
【問1】AさんとBさんが学校を出発して、学校から3000m離れた公園まで歩いて行った。最初にAさんが学校を出発し、一定の速さで公園に向かったが、買い物でコンビニ立ち寄り、そこで10分間過ごした。Aさんは、その後最初の速さで公園まで歩いた。Bさんは、Aさんの出発から20分後、一定の速さで歩き、2分30秒早く公園着いた。下の図は、AさんとBさんの歩く様子をグラフにしたものです。このとき、次の問いに答えなさい。
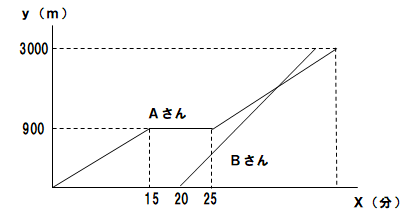
(1)Aさんの歩く速さを求めなさい。
(2)Aさんが学校を出発してからBさんに追いこされるまでの時間とAさん、Bさんがいる地点の間の距離を表したグラフを次から記号で1つ選べ。
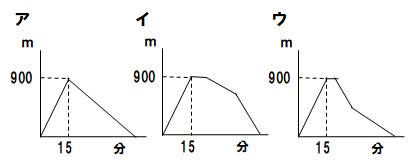
(3)AさんがBさんに追い越されたのが、学校から何m離れた地点か求めよ。求めるまでの過程も記述せよ。
【問2】図のように、AB=6cm、BC=8cm、AC=10cm、∠B=90°の直角三角形ABCがある。いま、点Pは毎秒2cmの速さで、頂点Bから頂点Cを通って頂点Aまで三角形の辺上を動く。頂点Bから出発してからx秒後の△ABPの面積をScm2とするとき、次の各問いに答えよ。
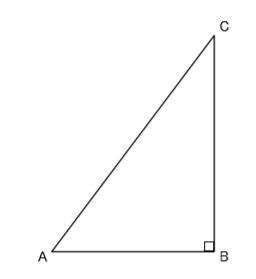
(1)点Pが辺BC上にあるとき、Sをxを用いて表せ。
(2)点Pが辺CA上にあるとき、Sをxを用いて表せ。
(3)S=12となるようなxの値を求めよ。
【問3】次の図1の四角形ABCDは、1辺8cmの正方形である。点Pは頂点Aを出発し、辺AB上を毎秒4cmの速さでA→B→A→B→Aと2往復する。点Qは頂点Cを出発し、辺CD上を毎秒1cmの速さでCからDまで進む。図2は、△PBCと△QBCの面積の関係を表すグラフである。点P、Qがそれぞれ頂点A、Cを同時に出発するとき、次の問いに答えよ。
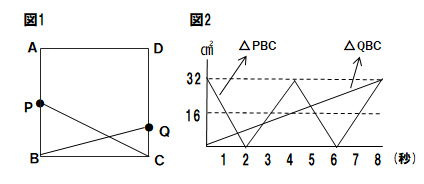
(1)2点P、Qが出発してからの4秒間の、時間と△PBCと△QBCの面積の差の関係を表したグラフをアからウより1つ選べ。ただし、差は、大きい方の面積から小さいほうの面積をひいたものとする。
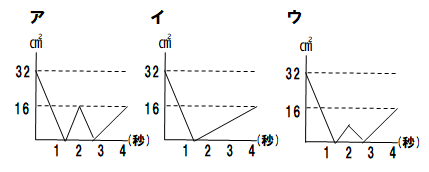
(2)△PBCと△QBCの面積の差がはじめて8cm2になるのは、 2点P、Qが出発してから何秒か求めよ。
(3)△PBCと△QBCの面積が3回目に等しくなるのは、2点P、Qが出発してから何秒か求めよ。
【問4】携帯電話のA社の料金とB社の料金は以下のようになっています。
<A社>
・基本料金2500円
・通話50分までは無料
・50分から100分までは1分間につき30円ずつ加算する
・100分以上については100分の代金のまま定額
<B社>
・基本料金2500円
・無料通話はなく, 1分間につき10円ずつ加算する
通話料がx分の時の料金をy 円とすると, A社の通話時間と料金の関係は次のグラフのようになります。このとき, 次の各問いに答えなさい。
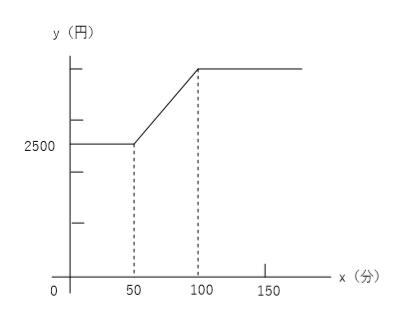
(1) A社において, 通話時間が80分と100分のときの料金を求めなさい。
(2) A社において, 次の各場合のとき, y をx の式で表しなさい。
① 0≦x≦50 のとき
② 50≦x≦100 のとき
③ 100≦x のとき
(3) B社において、yをxの式で表しなさい。
(4) A社の方がB社よりも料金が高くなるのは通話時間がどのようなときか求めなさい。
【問5】図のような、AB=6cm、AD=12cmの長方形ABCDがある。2つの点P,Qは以下の条件で動く。
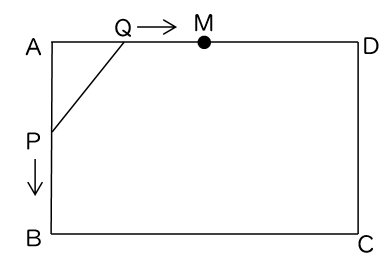
●点Qは点Pと同時に頂点Aを出発し、毎秒1cm の速さで辺AD上を辺ADの中点Mまで移動し、点Mに達するとそこで3秒間停止する。その後、毎秒2cmの速さで辺AD上を点Mから頂点Dまで移動し、頂点Dに達すると停止する。
点P,Qが同時に頂点Aを出発してからの時間をx秒、そのときの△APQの面積をycm2とするととき、次の問いに答えなさい。
(1)0≦x≦6におけるxとyの関係の式を、yをxの式で表せ。
(2)点P,Qが同時に頂点Aを出発してから頂点C,Dで停止するまでのxとyの関係を正しく表したグラフをア~ウより1つ選べ。
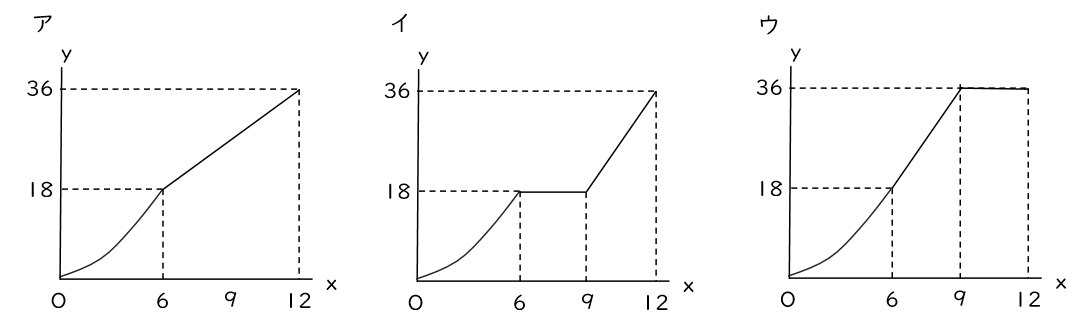
(3)点P,Qが同時に頂点Aを出発してから6秒後以降で、△APQと四角形QPCDの面積が等しくなるのは何秒後か求めよ。
一次関数の利用の練習問題の解答
●問1の解答
(1)分速60m
(2)ウ
(3)2400m
●問2の解答
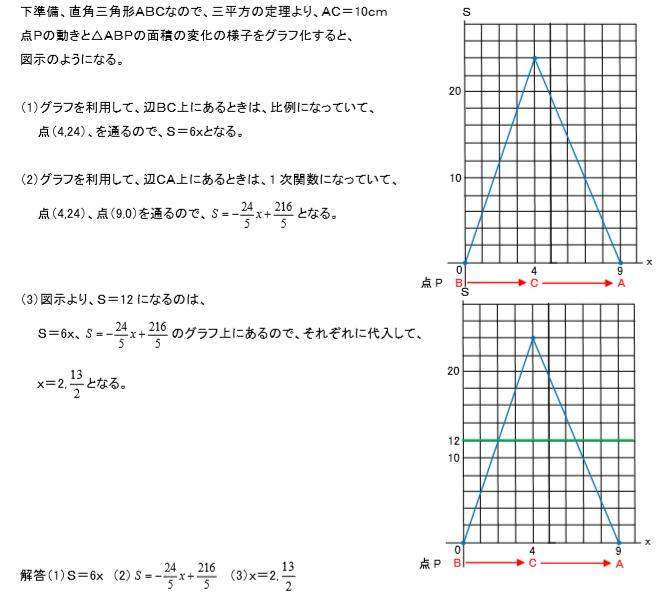
●問3の解答
(1)ウ
(2)6/5秒後
(3)24/5秒後
●問4の解答
(1)3400円、4000円
(2)①y=2500 ②y=30x+1000 ③y=4000
(3)y=10x+2500
(4)75分より長く150分未満のとき
(1)の解説
80分のときは2500円に30分間の通話料金が加算されるから
2500+30×30=3400 よって3400円
100分のときも同様に50分間の通話料金が加算されるから
2500+50×30=4000 よって4000円
(2)の解説
① 基本料金のままだからy=2500
② 1分間に30円ずつ加算されるから, 傾き30 よって
y=30x+bとおき、 これに、x=50 y=2500を代入して
2500=30×50+b b=1000 よってy=30x+1000
③ 100分以上は4000円で一定だからy=4000
(3) の解説
傾き10, 切片2500のグラフになるから、y=10x+2500
(4)の解説
点Pのx座標は、y=30x+1000とy=10x+2500の連立方程式代入法よりx=75すなわち75分
点Qのx座標は、y=10x+2500とy=4000の連立方程式代入法よりx=150すなわち150分
よって、75分より長く150分未満のとき
●問5の解答
(1)y=1/2x2
(2)イ
(3)10秒後

コメント
難しい応用問題ありがとうございました、問題1の(3)の太郎さんが不可解でしたが、勉強になりました。
よかった