中1数学「資料の活用(相対度数・代表値など)」についてまとめています。
資料の活用
まずは、資料の整理で出てくる用語とその求め方です。
相対度数
相対度数は、各階級の度数の全体に対する割合を、その階級の相対度数といいます。一般的に小数第2位まで求めます。割り切れないときは、小数第3位を四捨五入。
- 相対度数の計算=各階級の度数÷度数の合計
代表値
資料の値全体を代表する値を代表値といいます。
階級値
度数分布表で、各階級の真ん中の値を階級値といいます。
平均値
- 平均値=資料の個々の値の合計÷資料の個数
中央値
資料の値の大きさの順に並べたとき、その中央の値を中央値または、メジアンといいます。資料の個数が偶数の場合は、中央に並ぶ2つの値の平均をとります。
最頻値
資料の値の中で、もっとも頻繁に現れる値を最頻値とまたは、モードといいます。
範囲
資料の最大の値と最小の値の差を分布の範囲、またはレンジといいます。
- 範囲=最大値-最小値
資料の整理の度数分布表定期テスト予想問題
【問1】次の表は、あるクラスの小テストの得点をまとめたものです。次の問いに答えなさい。
| 階級(点) | 度数(人) |
|---|---|
| 5以上~10未満 | 6 |
| 10~15 | 4 |
| 15~20 | 12 |
| 20~25 | 16 |
| 25~30 | 2 |
| 計 | 40 |
- 平均値を求めなさい。
- 中央値がふくまれる階級を答えなさい。
- 最頻値を求めなさい。
- 20点以上とった人は何人か答えなさい。
- 10点以上15点未満の階級の相対度数を求めなさい。
- 25点以上30点未満の生徒は、全体の何%か求めなさい。
【問2】
次の表は、あるクラスの生徒30人について、ある月の保健室の利用回数を調べ、その結果を度数分布表に整理したものである。この表からわかることとして正しいものを次のア~オからすべて選び、記号で答えよ。
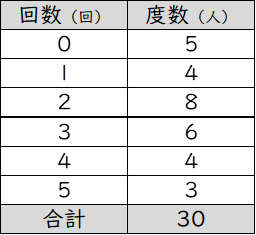
ア 回数の範囲は5回である。
イ 回数の平均値は2.5回である。
ウ 回数の中央値は2回である。
エ 回数の最頻値は3回である。
オ 回数が3回の階級の相対度数は0.20である。
資料の整理の度数分布表定期テスト予想問題の解答
【問1】
- 18点
- 15点以上20点未満の階級
- 22.5点
- 18人
- 0.1
- 0.5
【問2】
ア・ウ・オ
<度数分布表の問題>
標準的なレベルの問題です。定期テストでもよく見かける問題が列挙されています。がんばって解いてみましょう。

動画で解説①中1数学単元テスト 度数分布表の解答・解説
<ヒストグラムの問題>
標準的なレベルの問題です。こちらも定期テストでよく出題されるものとなっています。様々な代表値を求められるようになりましょう。
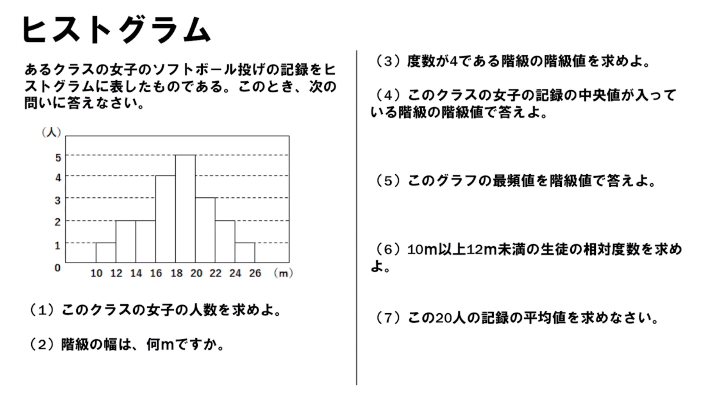
動画で解説②中1数学単元テスト ヒストグラムの解答・解説
以上が、中1数学「資料の整理の解き方のポイント」度数分布表・ヒストグラム 練習問題となります。

コメント