【2次関数】2点間の距離を求める練習問題です。2次関数の代表問題もあわせて問題として作成していますが、今回の中心は、「2点間の距離」にしぼって、深く学んでいきます。
●今回使う公式

三平方の定理と関数の融合の高校入試対策問題
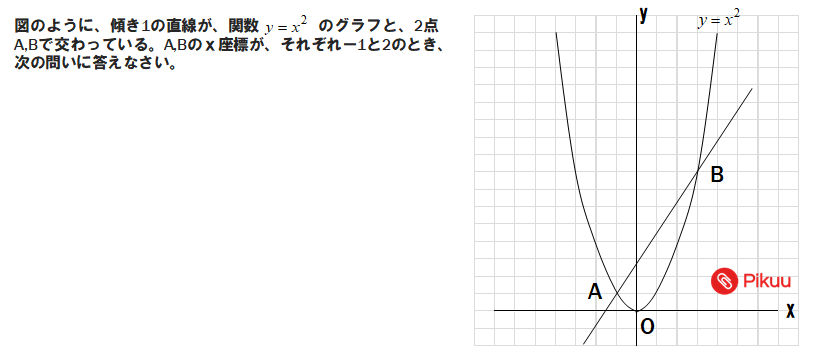
(1)直線ABの式を求めよ。
(2)線分ABの長さを求めよ。
(3)△AOBの面積を求めよ。
(4)原点Oを通り△AOBの面積を2等分する直線の式を求めよ。
三平方の定理と関数の融合の高校入試対策問題解説と解答
【解説】
(1)問題より、点A,Bのx座標がわかっているので、またそれぞれ、2次関数y=x2乗にあるので、代入してy座標を求めると、点A(-1,1)点B(2,4)となり2点を通る求める直線の式となる。
(2)斜めの長さなので三平方の定理を利用して解く。線分ABを斜辺として直角三角形を作ると、直角をはさむ辺がそれぞれ3となり、直角二等辺三角形になる。よって、特別な直角三角形より、1:1:1√2より求める長さは、3√2
(3)公式を使って、3×2÷2=3
(4)線分ABの中点つまり、(1/2,5/2)を通る直線の式を求めればよい。原点を通ることから、y=axに(1/2,5/2)代入して、aを求める。
【解答】
(1)y=x+2
(2)3√2
(3)3
(4)y=5/2x

コメント