平行四辺形の面積を二等分する直線を求める練習問題です。
ここで差がつく!➊平行四辺形の性質を理解しているか。特に、関数の問題においては、平行四辺形は向かい合う線分は平行なので、「傾き」が同じである。
➋平行四辺形の面積を2等分する直線は、必ず「対角線の交点」を通る。
➋平行四辺形の面積を2等分する直線は、必ず「対角線の交点」を通る。
平行四辺形の面積を二等分する直線を求める練習問題
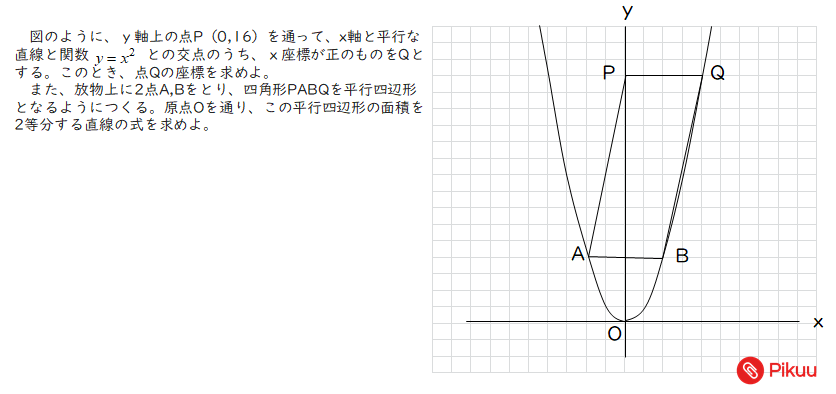
平行四辺形の面積を二等分する直線を求める解説
●Qの座標
<解法の手順>
1.Qのy座標は、平行四辺形ということから点Pのy座標と同じであるので、16となります。
2.Qのx座標は、y=x2上にあり、y=16ということから、y=16をy=x2に代入し、二次方程式を解く。それを解くと、x=±4。点Qのx座標はx>0より、x=4
よって、点Q(4,16)
●平行四辺形の面積を2等分する直線の式
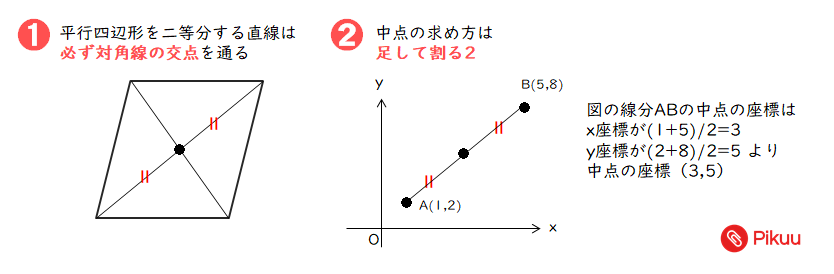
<解法の手順>
1.まず平行四辺形の面積を二等分する直線は、必ず対角線の交点を通るので、交点を求める。平行四辺形の対角線の交点は、おのおのの線分の中点(=平行四辺形の性質)なので、その中点を求める。
今その中点は、点A(-2,4)と点Q(4,16)なので、上の図の中点の求め方を参考に点(1,10)となる。
ちなみに、点Aが(-2,4)である理由ですが、線分PQ=4から線分AB=4である。点Aと点Bはy=x2上にあり、y軸に線対称から、それぞれx座標は、点A=-2、点B=2というわけである。
2.求める直線は、原点と点(1,10)を通るので、比例式となり、y=axに点(1,10)を代入してaを求める。それを解くと、a=10
よって、y=10xが答えとなる。
平行四辺形の面積を二等分する直線を求める解答
・Qの座標:点Q(4,16)
・平行四辺形の面積を二等分する直線:y=10x


コメント