中学数学「よく出る円と相似の融合問題」

円と相似の融合問題です。円周角の定理や相似の出現パターンを考慮しながら、解いていきましょう。また、直角三角形など直角する場合などは、三平方の定理を利用するときがほとんどです。

今回使う公式の例

円と相似の融合問題
1. 円と相似の融合問題の解説・解答

円と相似の融合問題

【問1】図のように、円Oの2つの弦AB、CDが点Pで交わっている。AB＝11ｃｍ、BC＝12ｃｍ、AD＝8ｃｍ、DP＝4ｃｍ、∠ CDB ＝65°のとき、次の問いに答えなさい。

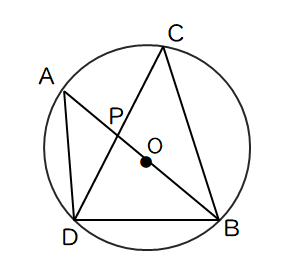
（1）△CPB∽△APDであることを証明せよ。
（2）∠ADPの大きさを求めよ。
（3）線分PBの長さを求めよ。
（4）線分PCの長さを求めよ。

【問2】図のように、円Oの円周上に点A,B,C,Dがる。点Eは、線分ADと線分BDの交点であり、点Fは、線分BAの延長と線分CDの延長が交わる点である。BC=12ｃｍ、AB＝AC、∠ABD＝∠CBDのとき、次の問いに答えよ。

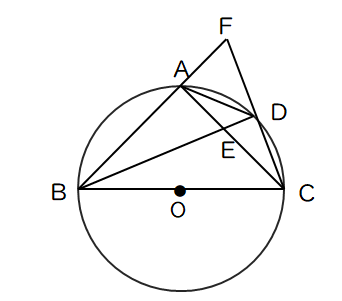
（1）△ABE≡△ACFであることを証明せよ。
（2）∠ADFの大きさを求めよ。
（3）△ACFの面積を求めよ。

円と相似の融合問題の解説・解答

【問1の解説】
（1）
△CPBと△APDにおいて、
弧BCの円周角より、∠PCB＝∠PAD…①
弧ACの円周角より、∠CPB＝∠APD…②

①②より
2組の角がそれぞれ等しいので、
△CPB∽△APD

（2）直径の円周角は90°を利用する。直径があって、90°が見当たらないときは、補助線を入れて90°を作ります。その後、共通する円周角は等しいなどから、図のように65°を記入。

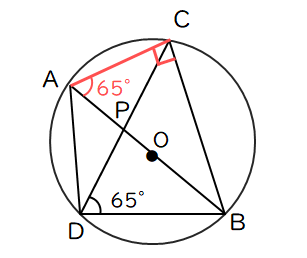
あとは、三角形の内角の和は180°から、180-90-65＝25°となる。

（3）相似を見つける。

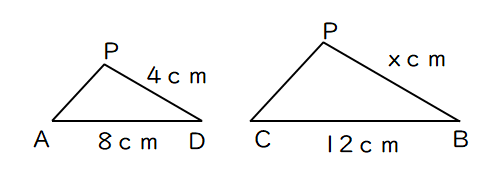
△CPB∽△APDより

PD:PB=AD:CB
4：ｘ＝8：12
x＝6

PB＝6ｃｍ

（4）相似をさらに探し求めていく。

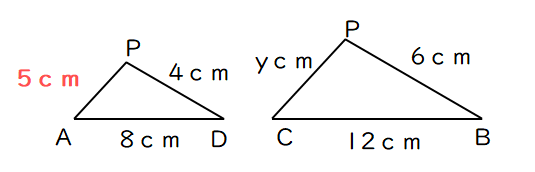
（3）よりPB=6ｃｍなので、PA＝AB-PB=11-6＝5ｃｍ

△CPB∽△APDより

PA:PC=AD:CB
5：ｙ＝8：12
ｙ＝15/2

PA＝15/2ｃｍ

【問2の解説】
（1）△ABEと△ACFにおいて

仮定より　AB＝AC…①
直径BCの円周角より、∠BAE＝∠CAF＝90°…②
弧ADの円周角より、∠ABE＝∠ACF…③

①②③より
1辺とその両端の角がそれぞれ等しいので
△ABE≡△ACF

（2）内接する四角形の定理を利用する。

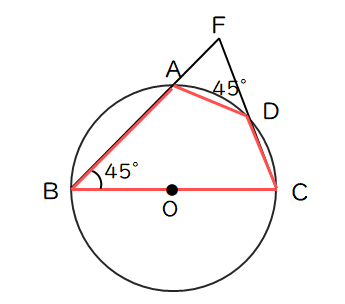
よって、45°

（3）わかっている長さを書き込んでいく。

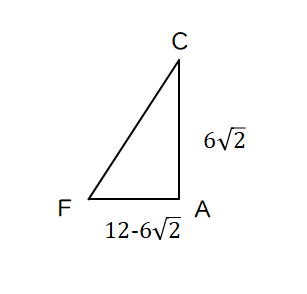
ACの長さは、△ABCが直角二等辺三角形より、特別な直角三角形を使い、6√2
FAの長さは、BF-ABとなる。AB＝ACなので、BF-AC（6√2ｃｍ）を求めることなる。BFは、BC（12ｃｍ）の長さと等しい。（※△BDF≡△BDCより）よって、FAは12-6√2