ここで差がつく!➊面積については、特に三角形において、底辺が等しければ、高さの比=面積比、高さが等しければ、底辺の比=面積比、相似であれば、相似比の2乗=面積比となるということは基本です。
➋➊の基本を合わせて使っていくのが高校入試や実力テストでは頻出です。
➋➊の基本を合わせて使っていくのが高校入試や実力テストでは頻出です。
●今回利用する公式

面積比の基本練習問題
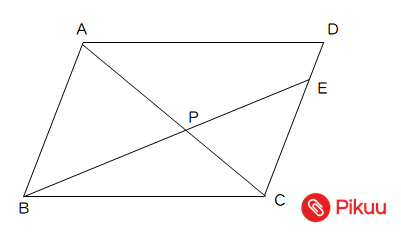
図のように、AB=4cm、BC=6cmの平行四辺形ABCDがあり、点Eは辺CDを1:3に分ける点である。また、点Pは線分ACとBEの交点である。このとき、△ABPと平行四辺形ABCDの面積の比を求めよ。
面積比の基本練習問題(解説・解答)
【解説】
最初の図の公式➌を利用して解けば、スムーズに解けます。今回は、点Aと点Eを結んであげることで、右に傾いたかたちで、上の図の公式➌の形ができます。以下のようになります。
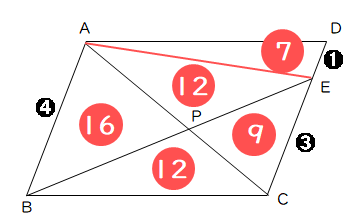
よって、△ABP:平行四辺形ABCD=16:56=2:7となります。
【解答】
△ABP:平行四辺形ABCD=2:7
面積比の標準練習問題
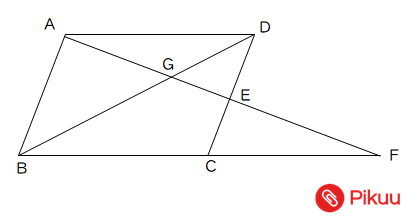
図のように、平行四辺形ABCDがある。辺CDの中点とEとして、直線AEと辺BCとの交点をF、AEとBDの交点をGとする。このとき、次の問いに答えなさい。
(1)△AGD:△BGFの面積の比を求めよ。
(2)△AGDと四角形GBCEの面積比を求めよ。
面積比の標準練習問題(解説・解答)
【(1)の解説】
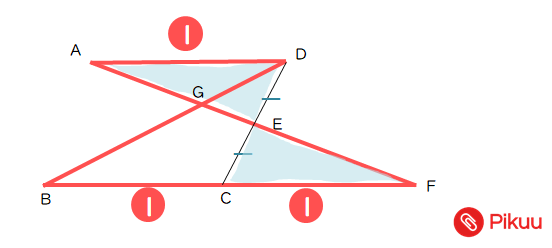
△AED≡△FECより、△AGDと△BGFは相似比1:2の相似となる。よって、面積は相似比の2乗=面積比より、1:4となる。
【(2)の解説】
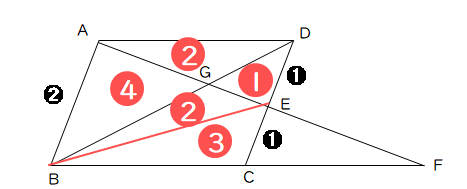
最初の公式➌を利用して、今回も解くことになります。点Bと点Eを結ぶことで利用できます。よって、上の図示のように△AGDと四角形GBCEの面積比は、2:5となります。
【解答】
(1)△AGD:△BGF=1:4
(2)△AGD:四角形GBCE=2:5

コメント
わかりやすいです!ありがとうございます!