関数における台形の二等分線を求める練習問題です。二次関数のグラフにおいて、台形の二等分線を求める問題は、理解を深めるために非常に有益な練習です。このような問題では、二次関数の特徴をしっかりと掴み、グラフの形状や対称性を意識しながら解くことが重要です。本記事では、台形の二等分線を求めるための基本的なステップを解説し、実際の練習問題を通して、解法を身につけていきます。二次関数の応用問題として、ぜひチャレンジしてみてください！
ここで差がつく！
台形を二等分する直線は上底の中点、下底の中点を求め、それぞれを結ぶ。そのまた中点を必ず通る。
台形を二等分する直線は上底の中点、下底の中点を求め、それぞれを結ぶ。そのまた中点を必ず通る。
●今回使う公式
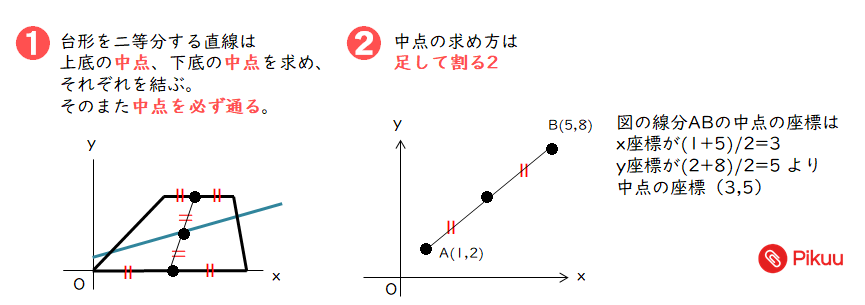
台形の二等分線を求める練習問題
（1）△ＤＡＥと△ＤＢＥの面積の比を最も簡単な整数の比で答えなさい。
（2）四角形ＡＤＢＣの面積を求めなさい。
（3）点（－2,1）を通りに、四角形ＡＤＢＣの面積を2等分する直線の式を求めなさい。
台形の二等分線を求める練習問題の解説・解答
【解説】
（1）△ＤＡＥと△ＤＢＥの面積の比は、高さが共通しているので
底辺の比が面積比となる。すなわち、
△ＤＡＥ：△ＤＢＥ＝ＡＥ：ＢＥとなる。
※ＡＥとＢＥは、斜めの線分より、三平方の定理で求める。
（2）四角形ＡＤＢＣは、台形になるので、（上底+下底）×高さ÷2となる。よって、（8+4）×6÷2＝36となる。
（3）の解法の手順
➊上底の中点＝線分ＡＢの中点（0、8）
➋下底の中点＝線分ＣＤの中点（0、2）
➌最後に、（0,8）と（0.2）の中点（0,5）を求める。
よって、求める直線は、点（-2,1）と点（0,5）を通る直線となり、y=2x+5
【解答】
（1）2：1 （2）３６ （4）y=2x+5
コメント