切断した立体の体積の求める練習問題です。上位校を目指す人は習得したい問題です。公式をうまく利用して解答を導きましょう。
●今回使う公式
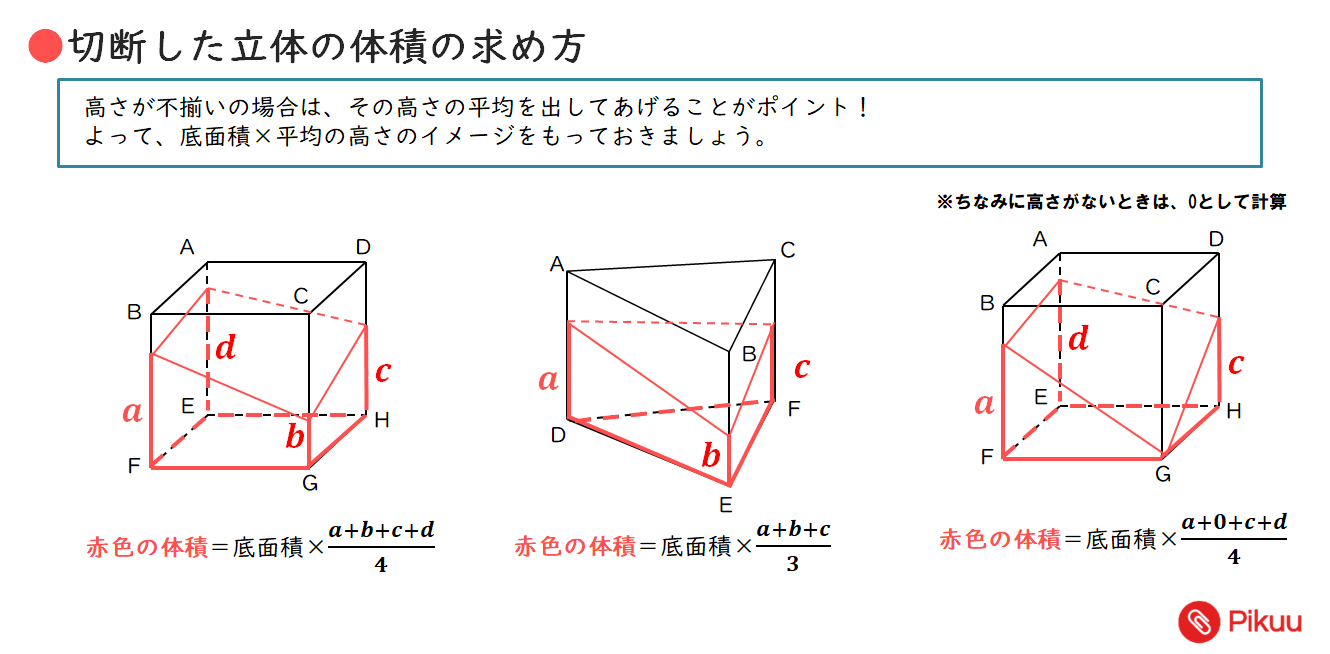
【問題】切断した立体の体積の求める練習問題
(1)1辺が8cmの立方体がある。4点PQRSで切断したとき、点Eを含む立体の体積を求めよ。なお、PF=6cm、QG=2cm、RH=5cm、SE=7cmである。
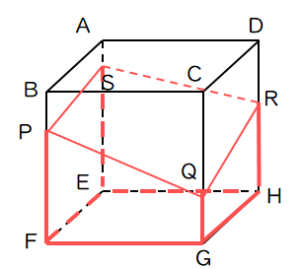
(2)底面が二等辺三角形の三角柱がある。AB=AC=6cm、BC=4cm、AD=5cm、BP=4cm、CQ=2cmのとき、四角錐A-BPQCの体積を求めよ。
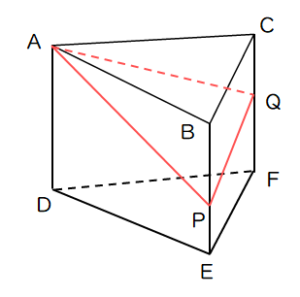
【解答・解説】切断した立体の体積の求める練習問題
【解説】
(1)公式を利用して解くと便利
・底面積 8×8=64
・高さの平均 (6+2+5+7)÷4=5
64×5=320cm3
(2)公式を利用して解くと便利
△ABCを底面として、
・底面積△ABC 4×4√2÷2=8√2
※高さの4√2は、三平方の定理を利用。Aから線分BCに垂線を下す。
・高さの平均 (0+4+2)÷3=2
8√2×2=16√2cm3
【解答】
(1)320cm3
(2)16√2cm3

コメント