中２数学公式「多角形の内角の和と外角の和」です。中学2年生の数学で学ぶ「多角形の内角の和と外角の和」は、図形問題を解くうえでの基礎となる重要な単元です。三角形や四角形だけでなく、五角形や六角形など、多角形全般に共通する性質を理解することで、より複雑な図形の問題にも対応できるようになります。また、外角の和が常に一定の値になるという性質は、効率よく解答を進めるうえでの鍵です。この記事では、内角の和と外角の和の計算方法や覚え方をわかりやすく解説し、理解を深めるための練習問題もご用意しました。効率よく学習を進めて、定期テストや入試に備えましょう！
多角形の内角の和と外角の和
ｎ角形では、1つの頂点から対角線をひいて、（ｎ-2）個の三角形に分けることができるから、内角の和は、180°×（ｎ-2）で求められます。一方で、多角形の外角の和は、360°です。これは、何角形であっても成り立ちます。
- ｎ各角形の内角の和+ｎ角形の外角の和＝180°×ｎ角形
ここで、(n-2）は、1つの頂点からひいた対角線によってできる三角形の数です。
| 項目 | ポイント |
|---|---|
| 内角の和の求め方 | 180∘(n – 2) ※nは多角形の辺の数 |
| 外角の和の特徴 | どの多角形でも外角の和は常に 360∘ |
| 三角形の内角の和 | 180∘ |
| 四角形の内角の和 | 360∘ |
| 五角形の内角の和 | 540∘ |
| 内角と外角の関係 | 1つの内角と隣接する外角の和は常に 180∘ |
| 覚え方のポイント | 内角の和は三角形に分割して考えるとわかりやすい。外角の和は必ず 360∘ と覚える！ |
| 練習のポイント | 多角形の形や辺の数に注目して式を当てはめる。正多角形では内角1つの大きさを求める練習も。 |
多角形の角度を求める公式テクニック
- 内角の和＝180（ｎ-2）°
- 外角の和＝360° （多角形の外角の和は、辺の数にかかわらず360°）です。
- 1つの内角+1つの外角＝180° （となりあう外角と内閣は180°）です。
- 1つの外角＝360÷n
- 1つの内角＝180-1つの外角＝180－（360/ｎ）
この5つの公式は、使いこなせるように演習をこなしましょう。とくに入試では、「1つの内角」を求めさせる問題が頻出です。
多角形の角度の練習問題
【問1】次の問いに答えなさい。
(1) 正八角形の内角の和を求めなさい。
(2) 正六角形の１つの内角の大きさを求めなさい。
(3) 正十角形の１つの外角の大きさを求めなさい。
(4) １つの外角の大きさが20度であるのは正何角形か。
(5) １つの内角の大きさが、１つの外角の大きさの3倍であるのは正何角形か。
【問2】次の図で∠xの大きさを求めなさい。
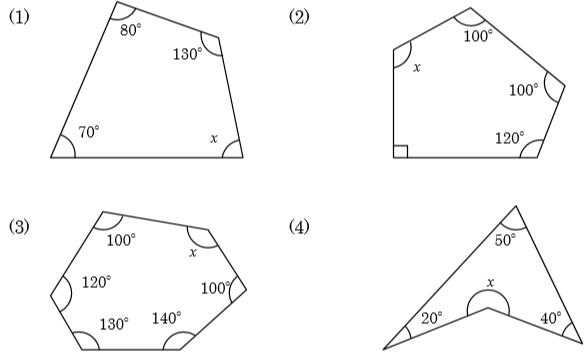
多角形の角度の練習問題解答
【問1】
(1)1080° →180°×(8－2)＝1080°
(2)120° →180°×(6－2)＝720° 720°÷6＝120°(別解)1つの外角が60°なので、180°－60°＝120°
(3)36° →360°÷10＝36°
(4)正十八角形 →360°÷20＝18°
(5)正八角形 →180°を3：1に分けると、180°÷(3＋1)＝45°（←外角） 360°÷45°＝8
【問2】
(1)80°
(2)130°
(3)130°
(4)250°
以上が、中２数学公式「多角形の内角の和と外角の和」となります。
コメント