中2数学「三角形の証明の練習問題」ポイント解説付

中2数学「三角形の証明の練習問題」ポイント解説付です。

【問題】三角形の証明の練習問題

■合同な図形の性質

• 合同な図形では、対応する線分の長さは、それぞれ等しい。
• 合同な図形では、対応する角の大きさは、それぞれ等しい。

■合同な表し方
△ABCと△EDFが合同であることを、記号≡を使って、△ABC≡△DEFのように表します。このとき、対応する順に並べます。

■証明のしくみ

• 証明…すでに正しいと認められていることがらを閑居として、仮定から結論を導くことです。
• 証明のしくみ…一般に、仮定から出発し、すでに正しいと認められたことを根拠に使って、結論を導きます。

■仮定と結論
数学では、「AならばBである」のような形で表されることがらがある。

「ＡならばＢである」のような形でいい表されることがらの、Ａの部分を「仮定」（与えられてあらかじめわかっていること）、Ｂの部分を「結論」（Ａから導こうとしていること）といいます。

■証明の進め方
1.結論（＝ゴール、目的）を確認する
この問題で言いたいことは何かを確認する

この問題の目的が何なのか？

• 「角度が等しいことを示すこと」なのか
• 「辺が等しいことを示すこと」なのか
• 「ある2辺が平行であること」　なのか

2.結論を達成するにはどうしたらいいか、その方法を考える
言いたいことを言うには、どうしたらよいか、その方法を考える

1. 「角度が等しいこと」を言うには→ 「２つの三角形が合同」を示せばよい（理由）合同な三角形の対応する角はそれぞれ等しいから
2. 「辺が等しいこと」を言うには→ 「２つの三角形が合同」を示せばよい（理由）合同な三角形の対応する辺はそれぞれ等しいから
3. 「ある２辺が平行であること」を言うには→ 「錯角または同位角が等しいこと」を示せばよい（理由）錯角、同位角が等しければ、2辺は平行だから

長さが等しい辺、大きさが等しい角をみつけたら、図に同じ印をいれるといいでしょう。三角形の合同を示すなら、三角形の合同条件のどれを使えばいいかを考える。

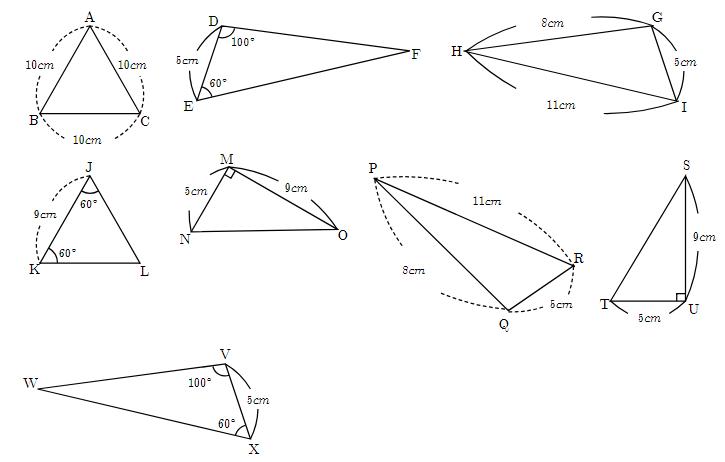
【問1】合同な図形を選ぶ練習問題

図の三角形を、合同な三角形の組に分けなさい。またそのときに使った合同条件を書きなさい。

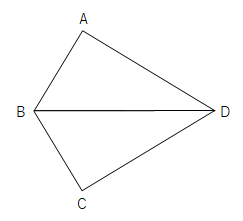
【問2】合同の証明の練習問題

次の図で、ＡＢ＝ＣＢ、ＢＤは∠ＡＢＣの二等分線です。このとき。ＡＤ＝ＣＤとなることを証明せよ。

【解答】三角形の証明の練習問題

【問1】合同な図形を選ぶ練習問題の解答

• △DEF≡△VXW　１組の辺とその両端の角がそれぞれ等しい。
• △GHI≡△QPR　３組の辺がそれぞれ等しい。
• △MNO≡△UTS　２組の辺とその間の角がそれぞれ等しい。

【問2】合同の証明の練習問題の解答

証明
△ＡＢＤと△ＣＢＤにおいて
仮定より　ＡＢ＝ＣＢ…①
仮定より　∠ＡＢＤ＝∠ＣＢＤ…②
共通な辺より　ＢＤ＝ＢＤ…③　（ＢＤは共通でも）
①②③より、2組の辺とその間の角がそれぞれの等しいので
△ＡＢＤ≡△ＣＢＤ
合同な図形では、対応する辺の長さは等しいので、
ＡＣ＝ＣＤ

▼その他の図形の証明問題を解く！
中2数学「平行四辺形に関する証明する練習問題」
中2数学「二等辺三角形に関する練習問題」
中2数学「直角三角形に関する証明問題の練習」