高校入試対策数学「円錐に関する対策問題」

円錐に関する練習問題です。入試でも頻出の立体です。多くの公式があり、出題パターンも多く存在することから問題も作成しやすいと同時に、受験生の学力を測るうえでも、良問となりうるからです。

●今回使う公式

円錐に関する練習問題

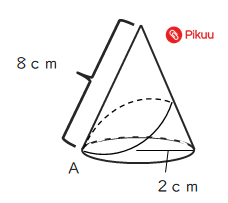
次の図のように底面の半径が2ｃｍ、母線の長さが8ｃｍの円錐について、次の問いに答えなさい。

（1）円錐の体積を求めよ。

（2）側面の展開図のおうぎ形の中心角を求めなさい。

（3）側面の展開図のおうぎ形の面積を求めよ。

（4）円錐の側面上をまわるように、点Aから点Aまでひもをかける。ひもの長さが最小となるときの長さを求めよ。

（1）高さがわからないので、まず高さを求める。頂点から垂線を下ろして三平方の定理を利用する。

高さをｈとすると
h²=8²-2²=64-4=60
h＝2√15

求める体積は　1/3×2×2×π×2√15
＝8/3√15π（3分の8ルｰト15）

（2）円錐を展開してできるおうぎ形の中心角なので、中心角をｘとして、「母線×中心角＝半径×360」を利用すると
8×ｘ＝2×360より、ｘ＝90°となる。

（3）側面んの展開図のおうぎ形＝円錐の側面積なので、「母線×半径×π」を利用して
8×2×π＝16πｃｍ²となる。

（4）

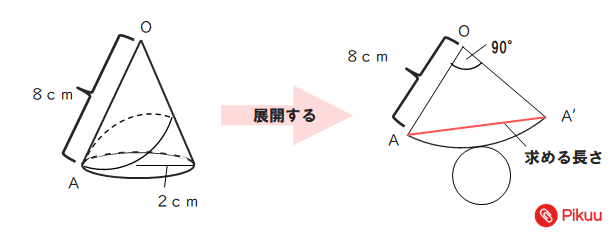
展開したあとで、ＡからＡまで直線に結んだ長さが最小となり、求める線分となります。
中心角が90°のことから△ＯＡＡ’は、直角二等辺三角形。1：1：√2より、求める長さは、8√2となる。

＜解答＞
（1）2√15ｃｍ
（2）90°
（3）16πｃｍ²
（4）8√2ｃｍ