知って得する中学数学の公式集（高校入試対応）です。随時更新していきますが、よく出る順に記事にしていきます。高校入試の数学で点数を伸ばすには 「中学数学の公式とテクニック」を正しく理解し、使いこなすこと が重要です。しかし、「公式が多すぎて覚えきれない…」「どの公式を重点的に勉強すればいいかわからない…」と悩んでいる人も多いのではないでしょうか？
本記事では、 高校入試でよく出る中学数学の公式と、その活用テクニックをわかりやすく解説 します。特に頻出の重要公式を厳選し、「これだけは覚えておけば安心！」という内容にまとめました。苦手な人でも実践しやすいコツや、実際の入試問題での使い方も紹介するので、ぜひ最後までチェックしてください！
この記事を読めば…
✅ 高校入試でよく出る中学数学の公式がひと目でわかる！
✅ 公式をどのように活用すればよいのかが理解できる！
✅ 効率よく勉強するためのコツが身につく！
数学の得点アップを目指して、今すぐ公式＆テクニックをマスターしましょう！
中学数学の公式テクニック一覧
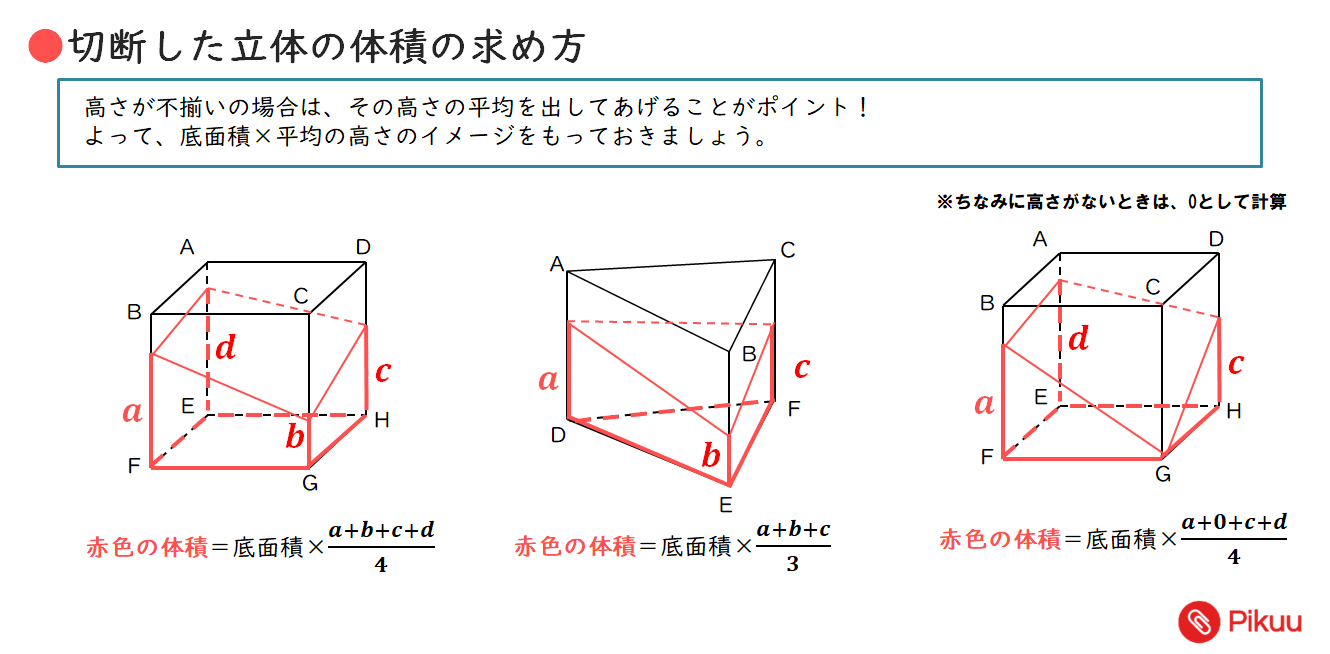
切断した立体の体積
不揃いの高さの平均を出すことで、早く体積が求められるようになります。
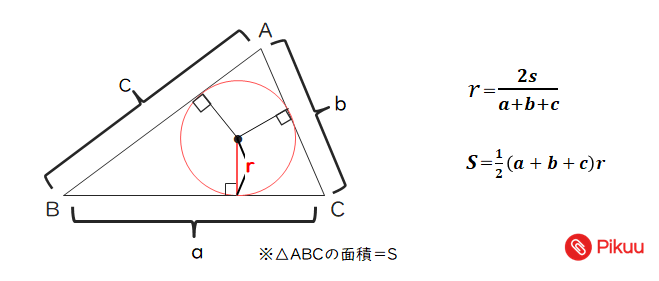
三角形に内接する円の半径の長さ
三角形のそれぞれの長さと面積を利用します。
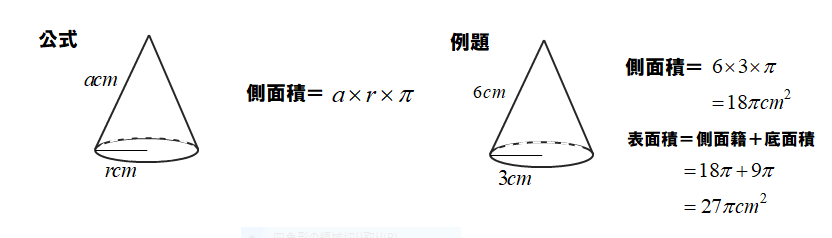
円錐の側面積
円錐は、展開するとおうぎ形の側面籍と円の底面積に分かれます。その側面積と底面積を足すと、表面積になります。
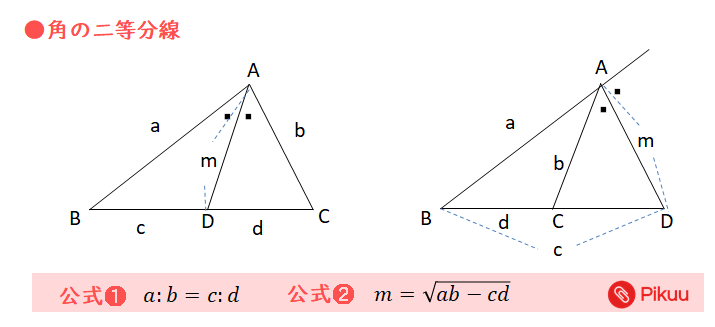
角の二等分線定理
入試でも頻出の定理です。使いこなせるようにしておきます。
面積比の公式
面積比に関する問題は、合否を左右する問題の1つです。合格を確実にするためにも、習得しておきたい公式です。
正三角形の面積
正三角形は、全ての辺が等しい三角形で、通常、1つの角が60度のなので、特別な直角形の1：2：√3を使用して、高さを求め、面積を求めます。
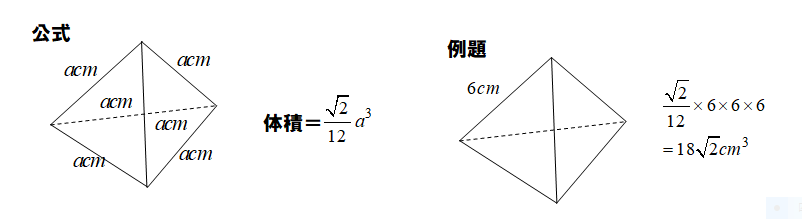
正四面体の体積
正四面体は、正三角形が4つ組み合わされた立体です。通常、頂点から垂線を下ろし、重心の性質や三平方を利用して、高さを求めて体積を求めます。
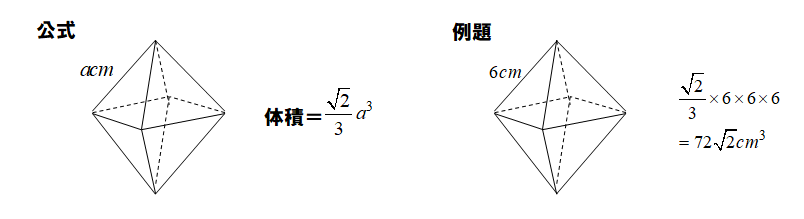
正八面体の体積
正八面体は、正四角すいが2つ上下にくっついた立体です。
コメント