中学3年理科。今日は力の合成と分解について学習します。
- レベル★☆☆☆
- 重要度★★★☆
- ポイント:矢印の先端から平行四辺形の作図
復習 中1理科「力のつり合いの重要ポイント」つり合いの条件と作図
力の合成
2つ以上の力を足し合わせ、一つの力に置き換える作業を、力の合成といいます。力を合成すると合力になります。
2つの力が同じ方向の場合、2つの力を足し合わせることで合力を求めることができます。2つの力が逆向きの場合、2つの力の差を求めることで合力を求めることができます。
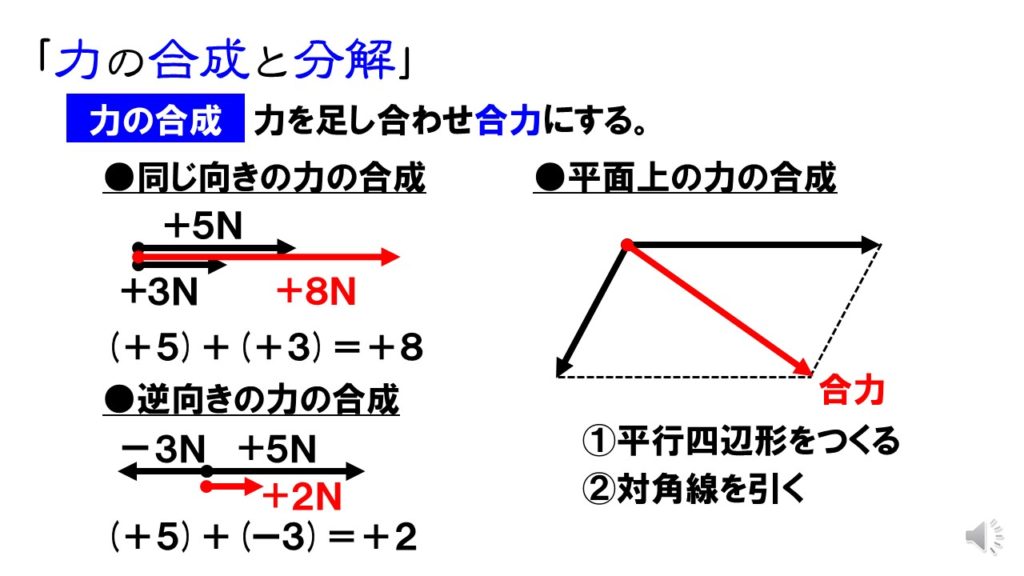
力の合成
次の力を合成し、合力の大きさを求めよ。
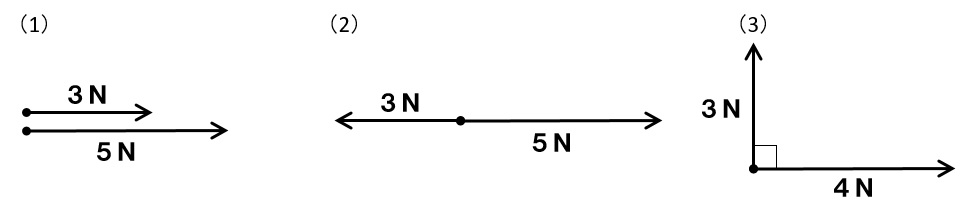
次の力を合成し、合力の大きさを求めよ。

解答
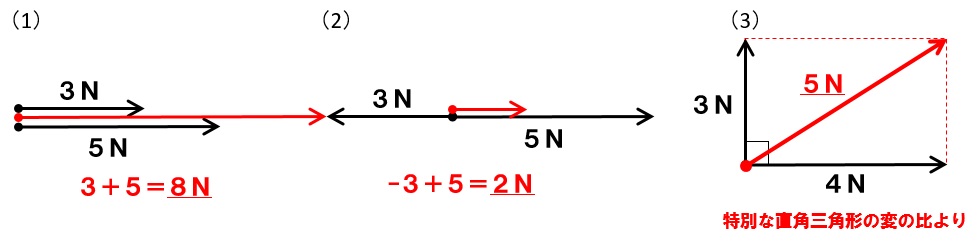
平行四辺形の法則
平面上の2力を合成する場合、2つの力がとなり合う2辺となるように平行四辺形を作図し、その対角線を引くことで合力を求めることができます。
力の分解
1つの力を、2つ以上の方向の力に置き換える作業を、力の分解といいます。力を分解すると分力が得られます。作業内容は、力の合成のまったく逆のことをするだけです。
分解しようとする1つの力が対角線になるように、平行四辺形を作図します。もとの力の作用点からとなり合う2辺に矢印をかけば、力の分解は終了です。
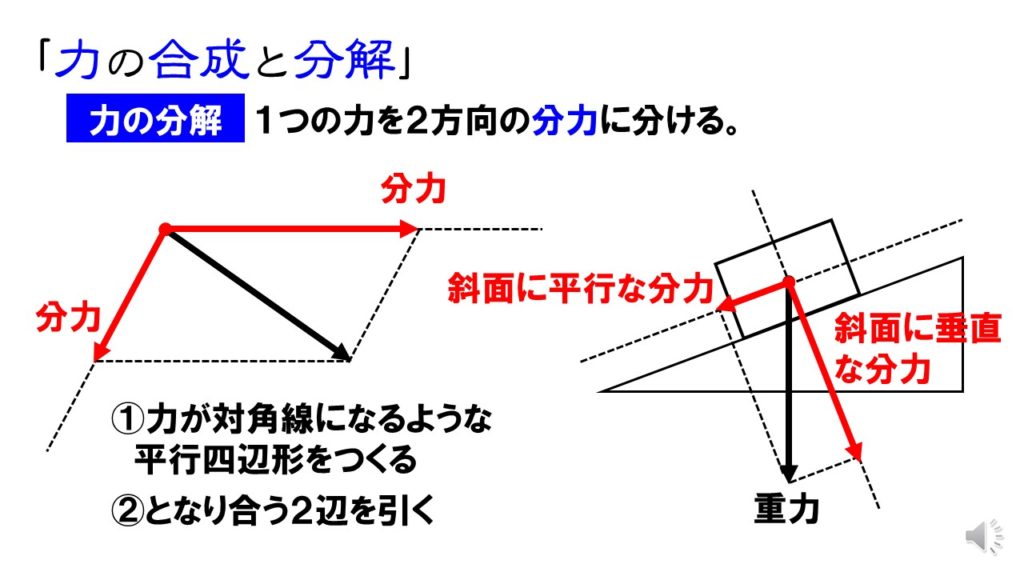
分解や合成の作図ポイント
作図で、平行四辺形をかく際のポイントは、矢印の先端から平行四辺形を書き出すということです。三角定規を使って平行四辺形をつくらなければいけない場合は、しっかりと練習を行っておきましょう。意外とかけない場合がありますよ。
力の分解
次の物体にはたらく重力を分解し、斜面に沿う分力と、斜面に垂直な分力の大きさを求めよ。ただし、図の1マスを2Nとする。
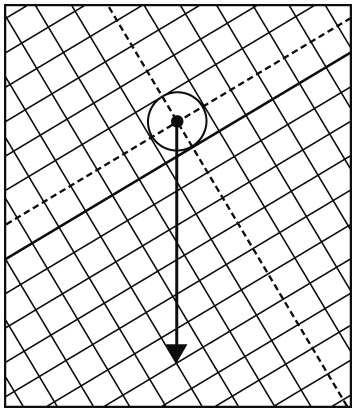
次の物体にはたらく重力を分解し、斜面に沿う分力と、斜面に垂直な分力の大きさを求めよ。ただし、図の1マスを2Nとする。

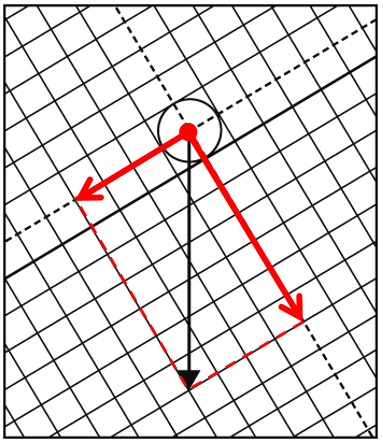
解答斜面に沿う分力:8.0N 斜面に垂直な分力:14N

コメント