中1数学「立体の表面積と体積の求め方と練習問題」

中１数学「いろいろな立体の表面積と体積の求め方」についてまとめています。

立体に表面積

表面積は、立体の表面全体の面積です。1つの底面の面積を底面積、側面全体の面積を側面積という。

• 角柱の表面積＝（底面積）×2+（側面積）
• 円柱の表面積＝（底面積）×2+（側面積）
• 角錐の表面積＝（底面積）+（側面積）
• 円錐の表面積＝（底面積）+（側面積）

point

• 円柱の側面は、底面積では、長方形になる。側面尾長方形の縦の長さは高さ、横の長さは底面の円の周の長さに等しくなる。
• 円錐の側面は、展開図ではおうぎ形になる。側面尾おうぎ形の半径は母線の長さ、おうぎ形の弧の長さは底面の円の周の長さに等しい。

立体の体積

• 直方体の体積＝縦×横×高さ
• 立方体の体積＝1辺×1辺×1辺
• ～柱の体積＝底面積×高さ
• ～錐の体積＝底面積×高さ÷3

球の側面積・体積

• 球の側面積＝4×π×半径×半径
• 球の面積＝（4×π×半径×半径×半径）/3

体積・表面積の基本問題

1. 1辺が3cmの立方体の体積と表面積を求めなさい。
2. 縦、横、高さがそれぞれ2cm、3cm、4cmの直方体の体積と表面積を求めなさい。
3. 底面の半径が4cm高さが5cmの円柱の体積と表面積を求めなさい。
4. 底面の半径が3cm高さが10cmの円錐の体積を求めなさい。
5. 底面が1辺5cmの正方形で高さが6cmの四角錐の体積を求めなさい。

体積・表面積の基本問題の解答

1. 体積27cm³/表面積54cm²
2. 体積24cm³/表面積52cm²
3. 体積80πcm³/表面積72πcm³
   側面の横の長さは底面の円周と同じなので8×π＝8πcm
   側面積＝8π×5＝40π
   底面積＝4×4×π＝16π
   表面積＝40π＋16π＋16π＝72π
4. 30πcm³
5. 50cm³

体積・表面積の練習問題

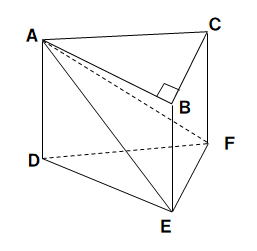
（1）下の図の三角柱で底面△ABCはAB=8cm,BC=6cm,AC=10cm,∠B＝90°の直角三角形で、AD=9cmのとき、点A、D、E、Fを頂点とする三角錐AーDEFの体積を求めよ。

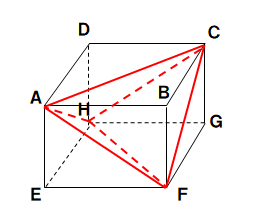
（2）図のように、1辺の長さが6ｃｍの立方体がある。4点A、C、F、Hを頂点とする立体の体積を求めよ。

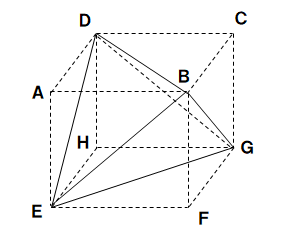
（3）次の図は、1辺が6ｃｍの立方体を、3点B,D,Cを通る平面と、3点B,E,Gを通る平面と、3点D,E,Gを通る平面で切断し、点D,F,Hを含む立体を取り除いてできた立体です。立体BDFGの体積を求めよ。

体積・表面積の練習問題の解答

(1)72cm³
(2)72cm³
(3)72cm³