高校入試対策数学「整数の規則性の練習問題」

整数の規則性の練習問題です。大きく2つ規則性があります。➊規則的に、2,4,6,8と増えていくときは、1次関数➋規則的に、1,4,9,16と増え方が増えていくときは、2次関数と踏まえておきましょう。

今回使う公式

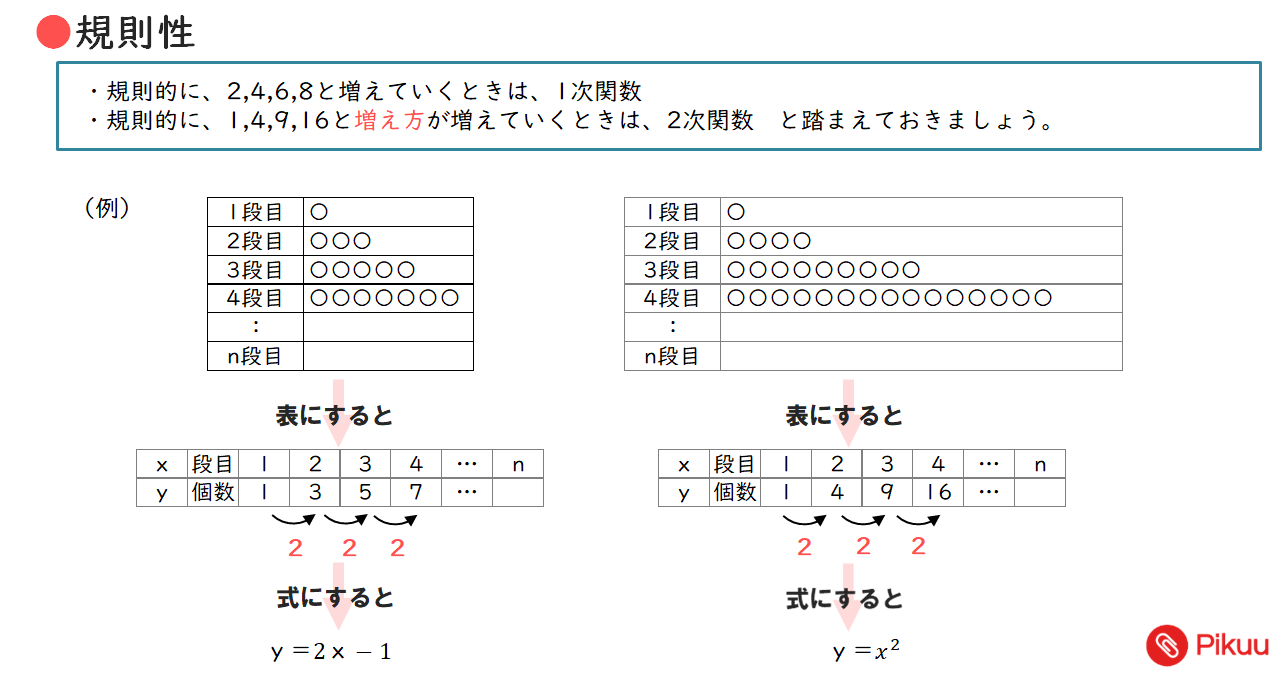
整数の規則性の問題

【問1】下の図のように、〇印を1段目、2段目、3段目…ある規則にしたがって、と記入していきます。このとき、次の問いに答えなさい。

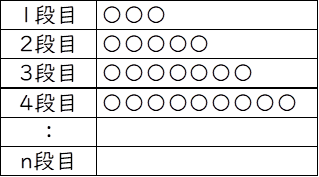
（1）7段目の〇の数を求めよ。
（2）ｎ段目の〇の数をｎを用いて表せ。
（3）〇の数が、79個になるときは、何段目か求めよ。

【問2】下の図のように、白の玉と黒の玉が、規則的に1番目、2番目、3番目と…並んでいくとき、次の問いに答えなさい。

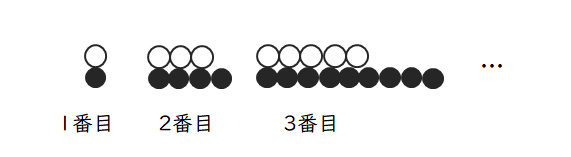
（1）黒の玉が81個になるときは何番目か。
（2）ｎ番目の白玉の数をｎを用いて表せ。
（3）白い玉と黒い玉の多いほうから少ないほうをひいた個数の差が81個になるのは、何番目か答えよ。

【解説】
問1　まず表を書いて、規則性の関係を式で表すと解きやすい。

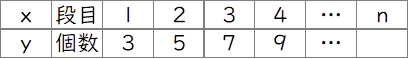
この表を式で表すと、増え方が一定（変化の割合が一定）なので、1次関数となるので、y=ax+bとおき、連立方程式なり、傾き2を代入して解くなりする。するとｙ＝2ｘ+1と表せる。

（1）ｙ＝2ｘ+1にｘ＝7（段目）を代入すると、ｙ（個数）＝15
（2）ｙ＝2ｘ+1にｘ＝ｎ（段目）を代入すると、ｙ（個数）＝2ｎ+1
（3）2ｘ+1＝79をとくと、ｘ（段目）＝39

問2
（1）黒玉の番目と個数の関係は、ｙ＝ｘ2と表せるので、ｘ2＝81となり、ｘ＝9
（2）2ｎ-1

（3）2番目以降、常に黒玉の個数が多いので、黒の個数ー白の個数＝81が成り立つ。
81個になるのが、ｎ番目とすると、黒の個数は、ｎ2　白の個数は、2ｎ-1と表せるので
ｎ2-（2ｎ-1）＝81
これを解くと
ｎ＝-8,10
ここで、ｎ>0なので、
8は問題に合わない。

よって、10番目が答えとなる。

【解答】
問1（1）15　（2）2ｎ+1　（3）39
問2（1）9　（2）2ｎ-1　（3）10