中3数学「式による証明の定期テスト予想問題」

中3数学「式による証明」について記述しています。

• レベル：標準
• 頻出度：定期テスト
• ポイント：証明の流れをつかむ

数の証明のパターン

主な出題パターンは、主に3つ。

• 倍数になることや割り切れることなど、「～に（なる）こと」
• 「～に等しくなること」
• 図形に関すること

式による証明問題

【問1（なることの証明問題）】
奇数の平方から１をひいた数は4の倍数であることを説明しなさい。

【問2（等しくなることの証明問題）】
連続する３つの整数がある。最大の整数と最小の整数の積は中央の整数の平方よりも１小さい数と等しくなることを説明しなさい。

【問3（新傾向の問題）】
下記の＜規則＞に従ったx+y+zの値が奇数を2乗した数になることを証明せよ。ただし、「ある自然数をｎとすると」から書き出しなさい。

【問4（図形の証明1）】
半径がa ｍの円形の土地の周囲に幅b ｍの道を下図のように作った。道の真ん中を通る線の１周をℓｍとし、道の面積をＳcm²とするこのとき、S＝bℓとなることを説明しなさい。

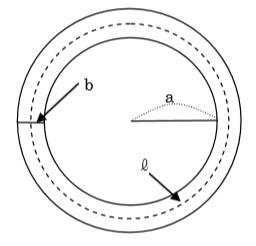
【問5（図形の証明2）】
下図のように、半径がｒｃｍの球が、円柱の底面と側面に接して入っている。

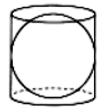
（1）円柱から球を取り除いた後の残った部分の体積を求めなさい。
（2）円柱の表面積と球の表面積の比が3：2となることを、証明しなさい。

式による証明問題の解答

【問1】
nを整数として、奇数は2n－1と表せる。

奇数の平方から1を引いた数は
(2n－1)²－1
＝4n²－4n＋1－1
＝4n²－4n
＝4(n²－n)
ここで、(n²－n)整数なので、4×（整数）となり
奇数の平方から１をひいた数は4の倍数である。

【問2】
nを整数として、連続する３つの整数はn－1、n、n＋1と表せる。

最大の整数と最小の整数の積は(n＋1)(n－1)＝n²－1…①
中央の整数の平方よりも１小さい数はn²－1…②

だから、最大の整数と最小の整数の積は中央の整数の平方よりも１小さい

【問3】
ある自然数をｎとすると、x=n²、y=(n+1)²、z=2n(n+1)と表せる。

x+y+z
=n²+(n+1)²+2n(n+1)
=4n²+4n+1
=(2n+1)²

ここでnは自然数なので、2n+1は奇数となる。
よって、x+y+zの値は奇数を2乗した数になる。

【問4】
S ＝π(a＋b)²－πa²
＝πa²＋2πab＋πb²－πa²
＝2πab＋πb²　…①
bℓ ＝b×ℓ
＝b×(2a＋b)×π
＝πb(2a＋b)
＝2πab＋πb²　…②
だから　①②より　S＝bℓになる。

【問5】