比合わせ（連比）の練習問題です。比合わせ（連比）は、高校入試でもよく出題される重要な単元のひとつです。異なる比をそろえて計算することで、数量の関係を正しく求めることができます。特に文章問題では、速さや割合、図形の比と絡めた応用問題が出題されることが多いため、しっかりと練習しておくことが大切です。
本記事では、比合わせの基本から応用までをわかりやすく解説し、実践的な練習問題を用意しました。高校入試に向けて、自信をつけていきましょう！上位校を目指す人であれば、習得しておきたいのが、この比合わせ（連比）です。
ここで差がつく！
➊線分が3つの分かれている問題などで使用し、比を合わせる。
➋比の合わせ方は、対象となる線分のどうしの最小公倍数で合わせるとよい。
➊線分が3つの分かれている問題などで使用し、比を合わせる。
➋比の合わせ方は、対象となる線分のどうしの最小公倍数で合わせるとよい。
●今回使う公式
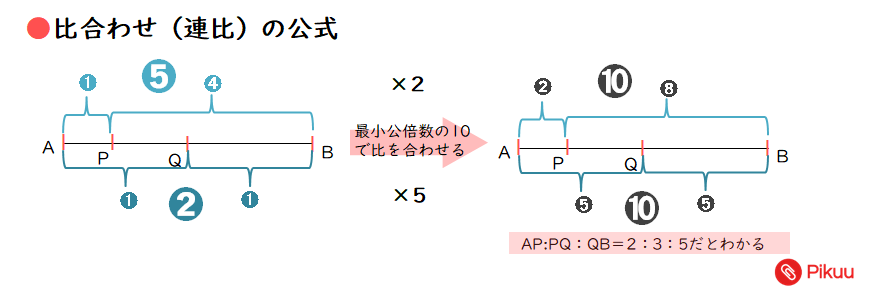
比合わせ（連比）の練習問題（基礎）
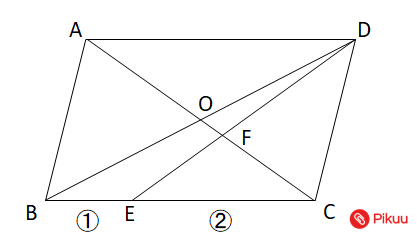
図の平行四辺形ABCDで、BE：EC＝1：2のとき、AO:OF:FCを求めなさい。
比合わせ（連比）の練習問題（基礎）の解答・解説
【解説】
△AOD≡△COB、△AFD∽△CFEから、それぞれの比を線分AC上に書き込み、比合わせ（連比）の公式を利用する。今回は以下の通りです。
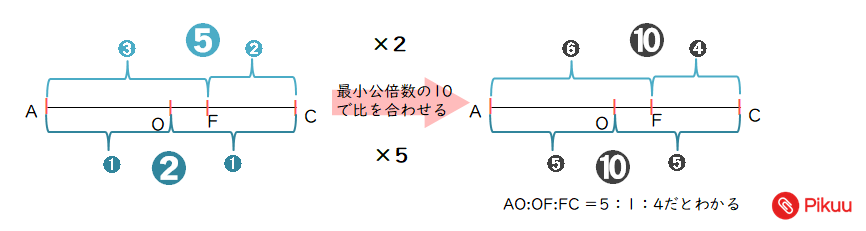
よって、AO:OF:FC＝5：1：4となる。
【解答】
AO:OF:FC＝5：1：4
コメント