中1数学「図形の移動」平行、回転、対称移動の作図まで仕上げよう!についてまとめています。
図形の移動とは?
図形の形と大きさを変えないで、位置だけを変えることを移動といいます。
平行移動
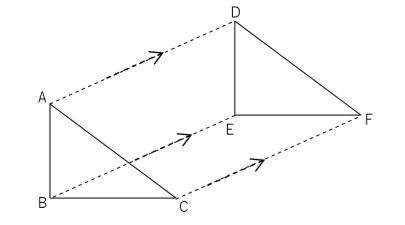
平行移動は、平面上で、図形を一定の方向に、一定の長さだけずらして、その図形を移すことです。平行移動では、対応する点を結んだ線分がそれぞれ平行で、その長さは等しいです。
- 対応する2点を結ぶ線分は、長さが等しく平行である。
- 対応する図形の線分は、長さが等しく平行である。
回転移動
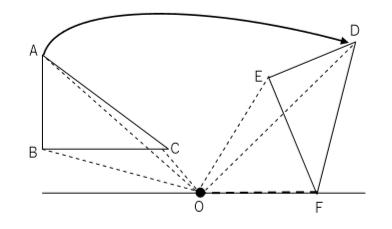
回転移動は、平面上で、図形を1つの点Oを中心として、一定の角度だけをまわして、その図形を移すことです。中心とした点Oを回転の中心といいます。特に、回転移動の中で180°の回転移動を点対称移動といいます。回転移動では、対称する点は、回転の中心から距離が等しく、回転の中心と結んできた角の大きさは、すべて等しいです。
- 対応する2点は、回転の中心からの距離が等しい。
- 図形のどの点も、回転の中心の回りに等しい角度だけ回転する。
対称移動
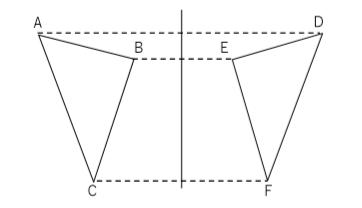
対称移動は、平面上で、図形を1つの直線lを折り目として、折り返して、その図形を移すことです。直線lを対称の軸といいます。
- 対応する2点を結ぶ線分は、対称の軸によって垂直に2等分される。
回転移動と角度練習問題
(1)下の図において、△ABCはAB=AC、∠BAC=40°の二等辺三角形である。また、△DBEは△ABCを点Bを中心として時計の針とは反対方向に回転移動したもので、点Eは△ABCの辺AC上にある。このとき、∠ABEの大きさを求めよ。
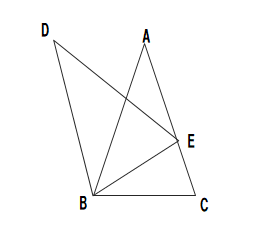
(2)△ADEは、△ABCを下の図のように、頂点Aを中心としてDA//BCとなるように回転させた三角形である。∠BAE=52°、∠BCA=62°のとき∠ABCの大きさを求めよ。
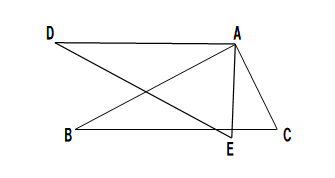
回転体と角度の解答
(1)30°
(2)33°


コメント