中3数学「三平方の定理の図形への利用の定期テスト対策問題」です。
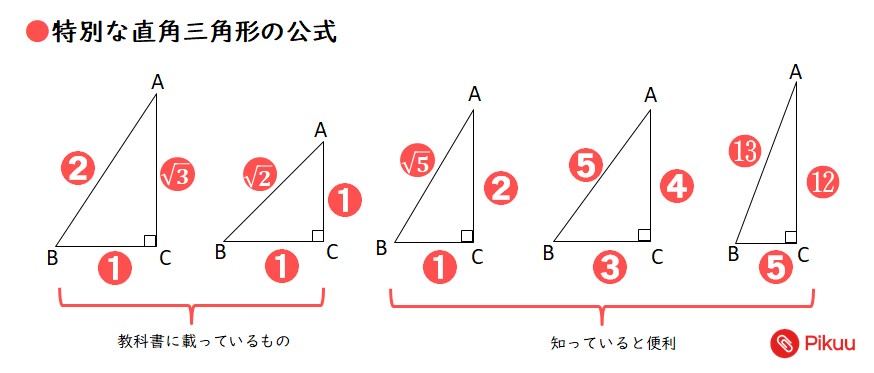
●今回利用する公式➊
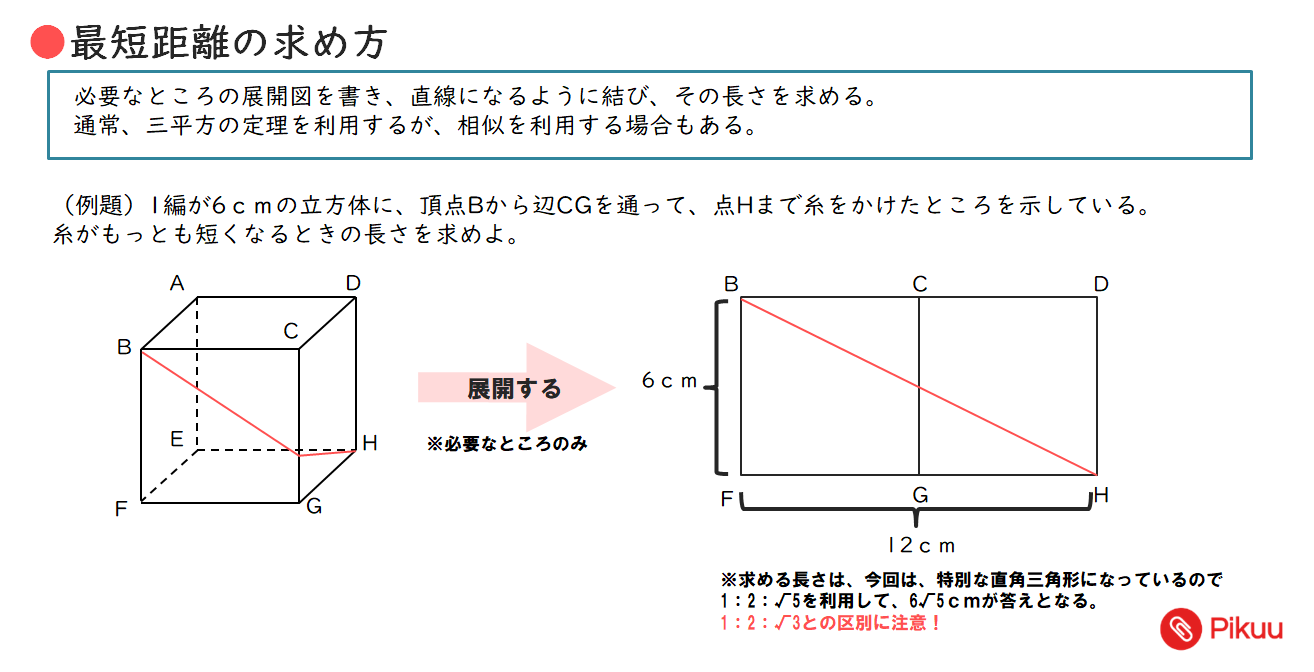
●今回使う公式➋
三平方の定理の図形への利用の定期テスト対策問題
【問1】次の図で、BC=10cm、DC=6cm、∠ABC=60°のとき、次の問いに答えなさい。
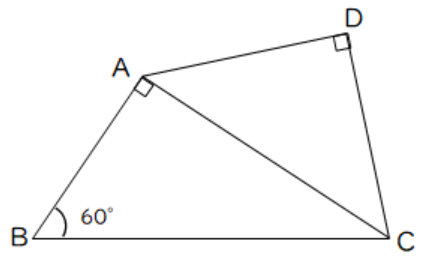
(1)ADの長さを求めなさい。
(2)四角形ABCDの面積を求めなさい。
【問2】次の△ABCで、AC=6cm、∠BAC=75°、∠ACB=60°のとき、次の問いに答えなさい。
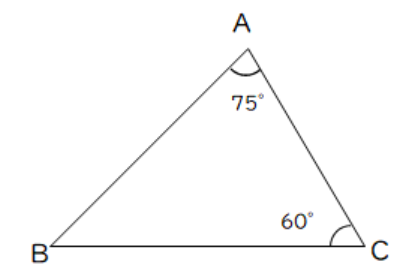
(1)ABの長さを求めよ。
(2)BCの長さを求めよ。
(3)△ABCの面積を求めよ。
【問3】次の△ABCで、BC=8cm、AB=7cm、∠ACB=120°のとき、次の問いに答えなさい。
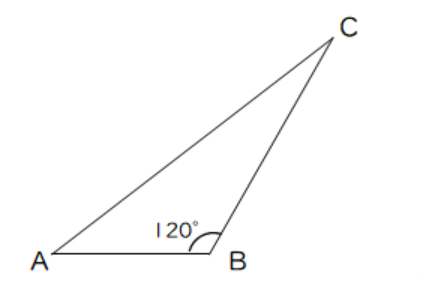
(1)ACの長さを求めよ。
(2)△ABCの面積を求めよ。
【問4】次の問いに答えなさい。
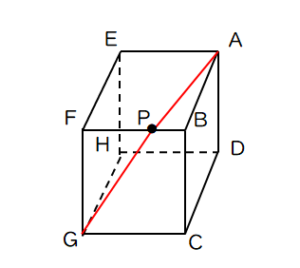
(1)図のように、AB=2cm,AD=6cm,AE=4cmの直方体である。点Pは辺BF上の点でAP+PGの長さが最小となるときの長さを求めよ。
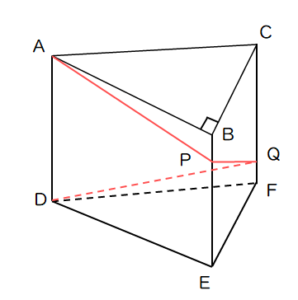
(2)図のように、AB=4cm、BC=3cm、AC=5cm、AD=6cm、∠ABC=90°の三角柱である。点P、点Qはそれぞれ辺BE、辺CF点で、AP+PQ+QDの長さが最も短くなるようにとった点である。このとき、 AP+PQ+QDの長さを求めよ。
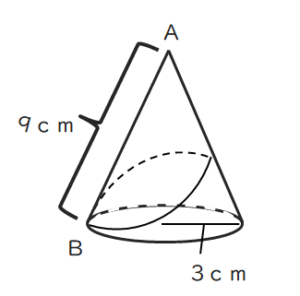
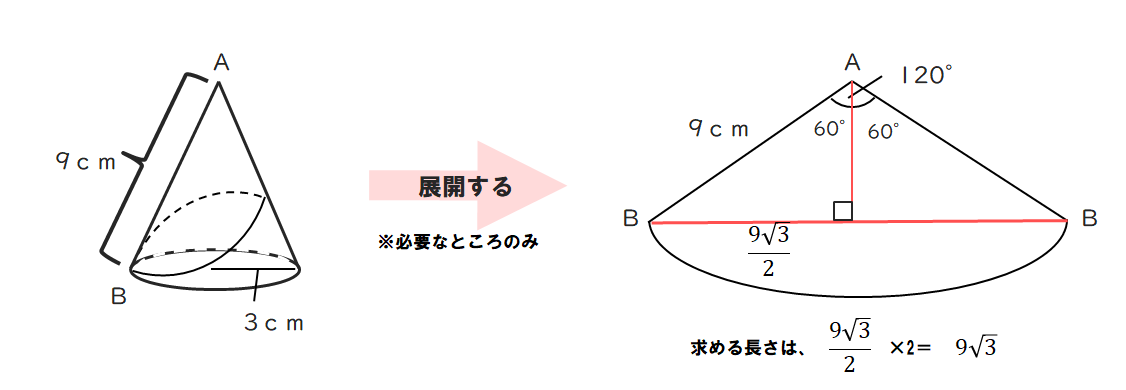
(3)母線9cm、半径3cmの円錐で、点Bから円錐の側面にそって一周し、点Bにもどる曲線をひく。この曲線がもっとも短くなるときの長さを求めよ。
特別な直角三角形練習問題解説・解答
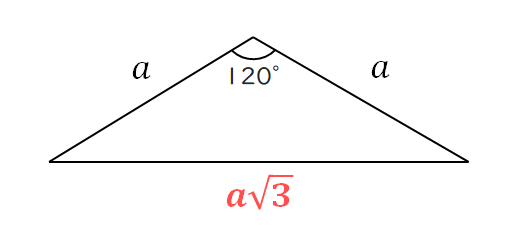
➋「120°」「75°」「135°」が出てきても垂線を下ろすことで、45°、60°が出現し、特別な直角三角形を利用できることが多々あります。
【問1】
(1)√39cm (2)25√3/2+3√39cm2
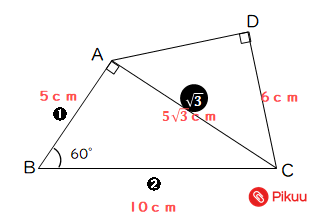
(1)特別な直角三角形の公式にあてはまることで、ACの長さ=5√3となる。このことにより、求めるADの長さは、直角三角形ACDに着目し、三平方の定理より√39cmとなる。
(2)四角形ABCD=△ABC+△ACDなので、それぞれ求める。
△ABC=5×5√3÷2=25√3/2
△ACD=6×√39÷2=3√39
よって、25√3/2+3√39cm2となる。
【問2】
(1)3√6cm (2)3√3+3cm (3)(27+9√3)/2cm2
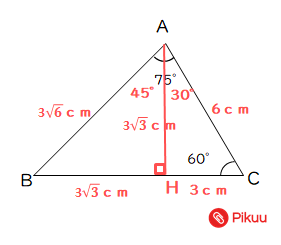
(1)(2)(3)図示したように、点Aから線分BCに垂線を下ろしその交点をHとすると、特別な直角三角形が2つできる。特別な直角三角形の公式を利用することで、(1)ABの長さ、(2)BCの長さ、(3)△ABCの面積は求める。
【問3】
(1)13cm (2)14√3cm2
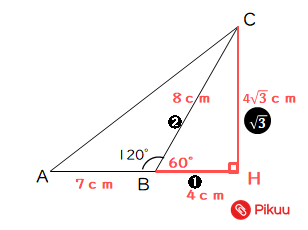
(1)(2)図示したように、点Cから垂線を下ろし、線分ABを延長した線分との交点をHとすると、特別な直角三角形が2つできる。特別な直角三角形の公式や三平方の定理を利用することで、(1)ACの長さ(△ACHの直角三角形に注目、線分CHは、特別な直角三角形の公式より求める。)(2)△ABCの面積を求めることができる。
【問4】
(1)4√5
(解説)展開して、三平方の利用を活用する。今回は、特別な直角三角形1:2:√5より、4√5
(2)6√5
(解説)展開すると以下のようになる。その後、三平方の利用を活用する。今回は、特別な直角三角形1:2:√5より、6√5
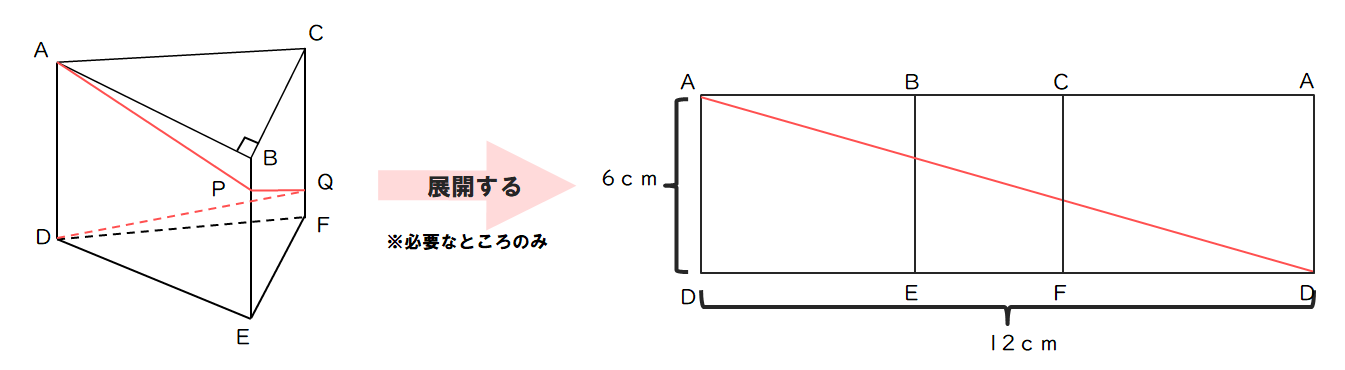
(3)9√3
(解説)展開すると以下のようになる。その後、展開したおうぎ形の中心角(頂角120°)から垂線を下すと1:2;√3の直角三角形が左右に2つできる。それを利用して長さを求める。
<別解>
以下のことを知っているとすぐ解答が導けます。


コメント