中学3年理科。イオンと化学変化で登場する中和の計算問題について学習します。
- レベル★★★★
- 重要度★★☆☆
- ポイント:水素イオンと水酸化物イオンの量に注目する!
授業用まとめプリントは下記リンクよりダウンロード!
授業用まとめプリント「完全中和の計算」
中和の計算問題
中和の計算問題は、みんなが苦手とする分野で、難問をつくろうと思えば簡単に作ることができる受験生泣かせの単元です。まずは基本的な計算だけでも解答できる力を身に付けましょう。
中和の計算パターンはおおよそ次の通りです。
- 完全中和点を求める問題
- 中和と塩の質量の問題
- 中和と気体の発生の問題
特に、酸とアルカリの水溶液が完全に打ち消し合う、完全中和点を求める問題は頻出です。濃度を変化させてくるパターンまで解けるようになると、ライバルと差をつけることができるようになります。また、グラフや表が頻繁に登場するので、その利用の仕方についても学習しましょう。
今日は、上記の3つのパターンのうち、完全中和に関する問題に挑戦します。水素イオンH⁺と水酸化物イオンOH⁻の数に注目して考えていきましょう。
完全中和点の計算
同じ濃度の塩酸と、水酸化ナトリウム水溶液を混ぜると、お互いの性質を打ち消し合う中和反応が起こります。もちろん、塩酸の量が多かったり、塩酸の濃度が高かったりすると、中和反応は起こりますが、中和後も水溶液中に水素イオンが残り酸性になります。
逆に、水酸化ナトリウム水溶液の量が多かったり、濃度が高かったりしても中和後の水溶液の性質はアルカリ性になります。
完全中和点とは、水素イオンと水酸化物イオンの数がちょうど同じになり、水溶液中に水素イオンと水酸化物イオンが無くなってしまった状態です。このとき水溶液の性質は中性になります。
完全中和の計算 濃度変化がない場合
まずは、実験中に水溶液の濃度が変化しないバージョンです。次の問題に挑戦してみてください。
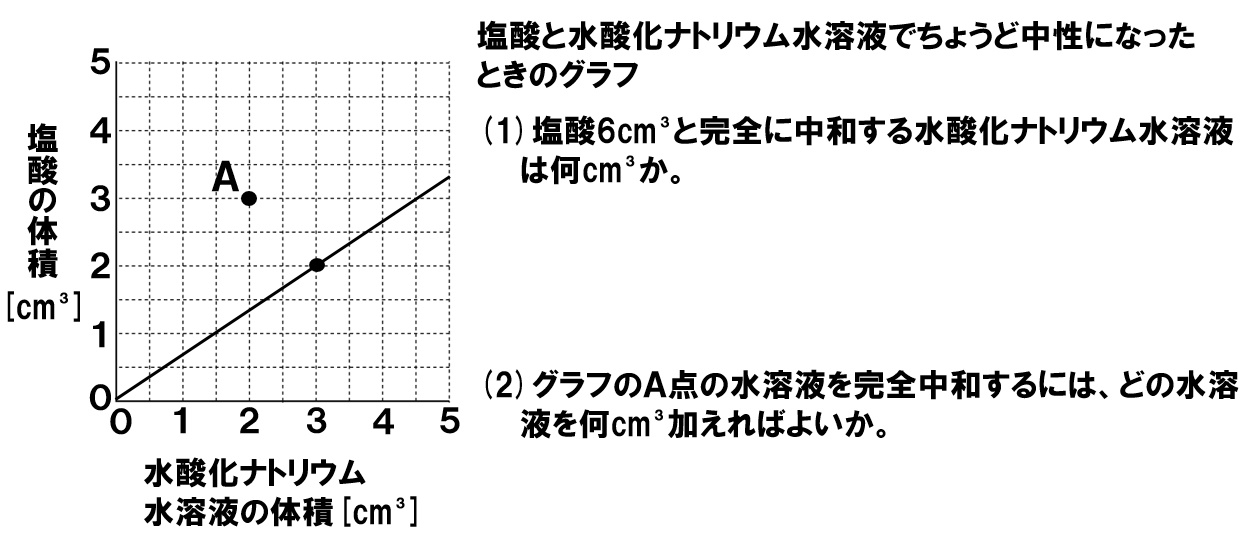
グラフの縦軸に塩酸の量、横軸に水酸化ナトリウム水溶液の量がとってあり、完全に中和した点をグラフで表したものです。原点を通る比例の関係になっていることがわかります。塩酸の量を2倍、3倍にすると、それを打ち消す水酸化ナトリウム水溶液の量も2倍、3倍になりますので、比例関係をうまく利用して問題を解いていきましょう。
(1)塩酸6cm³と完全中和する水酸化ナトリウム水溶液は?
グラフには、塩酸と水酸化ナトリウム水溶液が完全中和する直線が書いてあります。ちょうど、塩酸2cm³と水酸化ナトリウム水溶液3cm³が完全中和すると読めますので、塩酸6cm³を完全中和するには、
2:3=6:x
x=9cm³
であると求めることができます。
(2)どの水溶液をあと何cm³加えればよい?
グラフのA点は、塩酸3cm³に対して水酸化ナトリウム水溶液は2cm³混ぜてあります。水酸化ナトリウム水溶液が不足していることはわかるでしょうか。塩酸と水酸化ナトリウム水溶液は、体積比2:3で完全中和するので、塩酸3cm³を完全に打ち消すためには、
2:3=3:x
x=4.5cm³
必要であると計算できます。
水酸化ナトリウム水溶液は2cm³しか入っていないので、
4.5-2.0=2.5cm³
となります。
完全中和の計算 濃度が変化する場合
次は、水溶液の濃度を考えないといけない問題です。この場合は、水溶液中に含まれる水素イオンH⁺と水酸化物イオンOH⁻の量に注目して解いていくことになります。次の問題に挑戦してみてください。
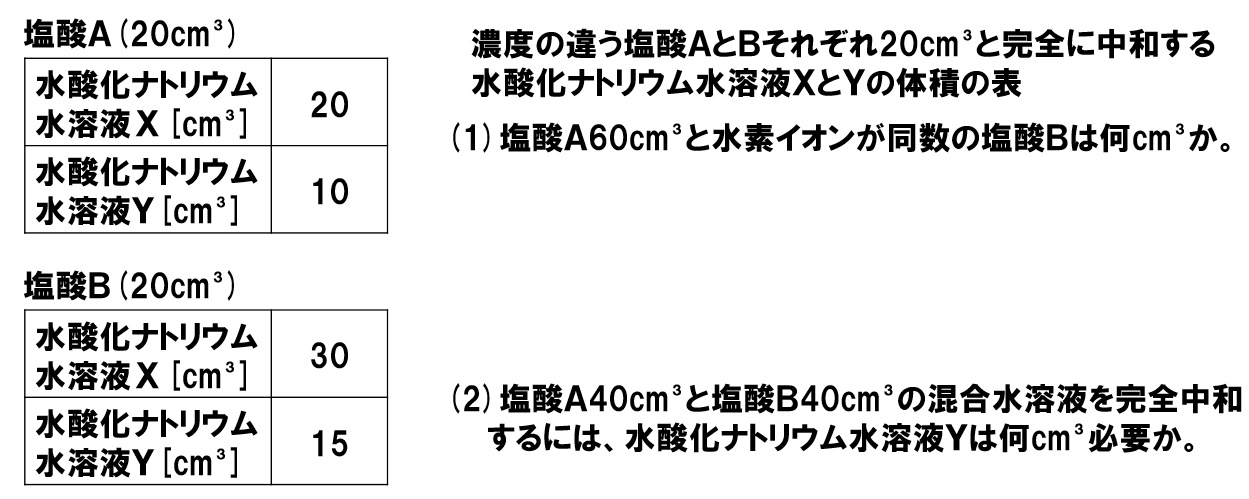
(1)水素イオンの数が等しい水溶液
塩酸Aの中の水素イオンH⁺の数を勝手に20個と仮定します。そうすると、これと完全に打ち消し合う水酸化ナトリウム水溶液X20cm³の中には、水酸化物イオンOH⁻が20個あることになります。また、水酸化ナトリウム水溶液Y10cm³の中にも、水酸化物イオンOH⁻が20個あることになります。
水酸化ナトリウム水溶液X20cm³中に水酸化物イオンOH⁻が20個あるのだから、水酸化ナトリウム水溶液X30cm³中に水酸化物イオンは30個あります。これと完全に打ち消し合う塩酸Bの中には、水素イオンH⁺が30個あることになります。
塩酸A20cm³の中にH⁺は20個あるから、塩酸A60cm³の中にH⁺は60個あります。
塩酸B20cm³の中にH⁺は30個あるから、H⁺を60個にするためには塩酸Bは40cm³必要であるとわかります。
(2)濃度が違う水溶液を混ぜた場合
塩酸A20cm³中にH⁺が20個あるので、塩酸A40cm³中にH⁺は40個あることになります。
また、塩酸B20cm³中にH⁺が30個あるので、塩酸B40cm³中にH⁺は60個あることもわかります。
混ぜ合わせた塩酸の中に、H⁺は合計100個となるので、これを完全に打ち消すための水酸化ナトリウム水溶液Yの中にもOH⁻は100個必要になります。水酸化ナトリウム水溶液Y10cm³中にOH⁻は20個あるので、水酸化ナトリウム水溶液Yは50cm³必要であるとわかります。
このように、水素イオンH⁺と水酸化物イオンOH⁻の数を考えて解いていけば、難しい中和の計算もすらすらと解けるようになります。


コメント