中学2年生の数学で学ぶ「直角三角形の合同の証明」は、テストで頻出の重要単元です。しかし、「どの条件を使えばいいのかわからない」「証明の書き方が難しい」と感じる人も多いのではないでしょうか？
この記事では、直角三角形の合同条件をわかりやすく解説し、証明のポイントを丁寧に説明します。また、テストによく出る練習問題も用意しているので、しっかり演習して証明問題を得意にしましょう！
【問題】直角三角形の合同の証明の練習問題
直角三角形とは三角形のうち、90°（直角）がある三角形を直角三角形という。
直角三角形で直角に対する辺を斜辺という。
直角三角形の合同条件②…斜辺と他の1辺がそれぞれ等しい。
【問1】直角三角形の練習問題
次の図で、AB＝ACの二等辺三角形ABCで、頂点Bから辺ACに垂線をひき、その交点をD、また、頂点Cから辺ABに垂線をひき、その交点をEとします。このときAD＝AEになることを証明せよ。
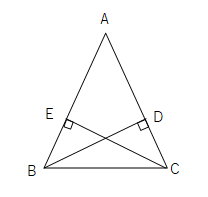
【問2】直角三角形の練習問題
図でPOは∠AOB の二等分線である。∠OAP=∠OBP=90°のときAP=BPとなることを証明しなさい。
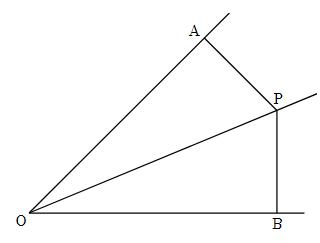
【問3】直角三角形の練習問題
次の四角形ABCDは、正方形である。辺BC上に点F、辺CD上の延長に点QをAP＝AQとなるようにとるとき、△ABPと△ADQが合同であることを証明せよ。
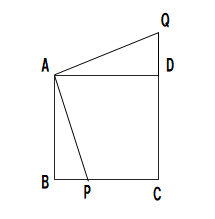
【解答】直角三角形の合同の証明の練習問題
【問1】直角三角形の練習問題の解答
△ABDと△ACEにおいて
仮定より AB＝AC…①
仮定より ∠ADB＝∠AEC＝90°…②
共通な角より ∠BAD＝∠CAE…③
①②③より 直角三角形の斜辺と1つの鋭角がそれぞれ等しいので、
△ABD≡△ACE
合同な図形は対応する辺は等しいので、AD＝AE
【問2】直角三角形の練習問題の解答
△AOPと△BOPにおいて
OP=OP(共通)
∠AOP=∠BOP(PO は∠AOB の二等分線）
∠OAP=∠OBP=90°(仮定)
よって直角三角形の斜辺と 1 つの鋭角がそれぞれ等しいので△AOP≡△BOP
合同な三角形の対応する辺は等しいので AP=BP となる
【問3】直角三角形の練習問題の解答
△ABPと△ADQにおいて
仮定より、AP＝AQ…①
四角形ABCDは正方形より、AB＝AD…②
また、∠ABP＝∠ADC＝90°…③
ここで、∠ADQ＝180°-∠ADC＝90°…④
③④より、∠ABP=∠ADQ＝90°…⑤
①②⑤より、直角三角形の斜辺と他の1辺がそれぞれ等しいので、
△ABP≡△ADQ
コメント